Bài 5 trang 11 SGK Toán 9 tập 2
Tóm tắt bài
Đề bài
Đoán nhận số nghiệm của hệ phương trình sau bằng hình học:
a) \( \left\{ \matrix{2{\rm{x}} - y = 1 \hfill \cr x - 2y = - 1 \hfill \cr} \right. \); b) \( \left\{ \matrix{2{\rm{x + }}y = 4 \hfill \cr - x + y = 1 \hfill \cr} \right. \)
Hướng dẫn giải
+) Đưa các phương trình đã cho về dạng \(y=ax+b\) và \(y=a'x+b'\).
+) Vẽ đường thẳng biểu diễn tập nghiệm của hai phương trình trên cùng một hệ tọa độ.
+) Tìm giao điểm.
+) Thử lại tọa độ giao điểm đó vào hệ hai phương trình ban đầu. Nếu thỏa mãn thì là nghiệm của hệ.
Lời giải chi tiết
a) Ta có:
\(\left\{ \matrix{
2x - y = 1 \hfill \cr
x - 2y = - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = 2x - 1 \ (d)\hfill \cr
y = \dfrac{1}{2}x + \dfrac{1}{2} \ (d') \hfill \cr} \right.\)
+) Vẽ \((d)\): \(y=2x-1\)
Cho \(x = 0 \Rightarrow y = -1\), ta được \(A(0; -1)\).
Cho \(y = 0 \Rightarrow x = \dfrac{1}{2}\), ta được \(B{\left(\dfrac{1}{2}; 0 \right)}\).
Tập nghiệm của phương trình là đường thẳng đi qua hai điểm \(A,\ B\).
+) Vẽ \((d')\): \(y=\dfrac{1}{2}x+\dfrac{1}{2}\)
Cho \(x = 0 \Rightarrow y = \dfrac{1}{2}\), ta được \(C {\left(0; \dfrac{1}{2} \right)}\).
Cho \(y = 0 \Rightarrow x = -1\), ta được \(D = (-1; 0)\).
Tập nghiệm của phương trình là đường thẳng đi qua hai điểm \(C,\ D\).
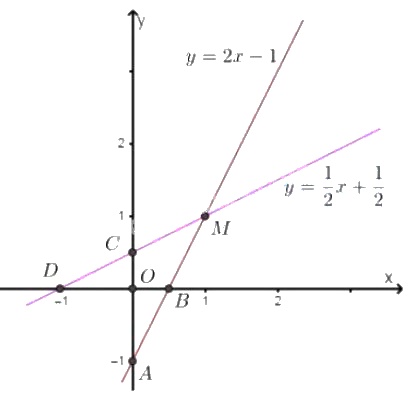
+) Quan sát hình vẽ, ta thấy hai đường thẳng cắt nhau tại điểm có tọa độ \(M( 1, 1)\).
Thay \(x = 1, y = 1\) vào các phương trình của hệ ta được:
\(2 . 1 - 1 = 1\) (thỏa mãn)
\(1 - 2 . 1 = -1\) (thỏa mãn)
Vậy hệ phương trình có một nghiệm \((x; y) = (1; 1)\).
b) Ta có:
\(\left\{ \matrix{
2x + y = 4 \hfill \cr
- x + y = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = - 2x + 4 \ (d) \hfill \cr
y = x + 1 \ (d') \hfill \cr} \right.\)
+) Vẽ \((d)\): \(y=-2x+4\)
Cho \(x = 0 \Rightarrow y = 4\), ta được \(A(0; 4)\).
Cho \(y = 0 \Rightarrow x = 2\), ta được \(B(2; 0)\).
Tập nghiệm của phương trình là đường thẳng đi qua hai điểm \(A,\ B\).
Vẽ \((d')\): \(y=x+1\)
Cho \(x = 0 \Rightarrow y = 1\), ta được \(C(0; 1)\).
Cho \(y = 0 \Rightarrow x = -1\), ta được \(D(-1; 0)\).
Tập nghiệm của phương trình là đường thẳng đi qua hai điểm \(C,\ D\).
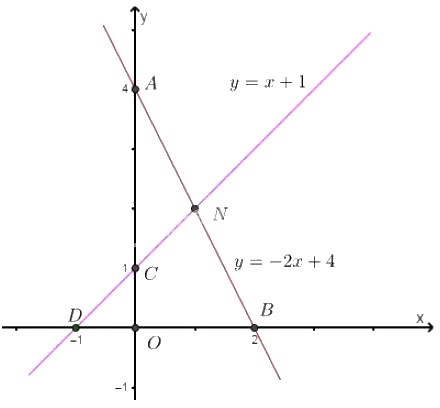
Quan sát hình vẽ, ta thấy hai đường thẳng cắt nhau tại điểm có tọa độ \(N(1;2)\).
Thay \(x = 1, y = 2\) vào các phương trình của hệ ta được:
\(2 . 1 + 2 = 4\) và \(-1 + 2 = 1\) (thỏa mãn)
Vậy hệ phương trình có một nghiệm \((x; y) = (1; 2)\).
Copyright © 2021 HOCTAP247
