Giải bài 7 trang 12 - Sách giáo khoa Toán 9 tập 2
Tóm tắt bài
Đề bài
Cho hai phương trình 2x + y = 4 và 3x + 2y = 5.
a) Tìm nghiệm tổng quát của mỗi phương trình trên.
b) Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong cùng một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.
Hướng dẫn giải
Hướng dẫn:
- Nghiệm tổng quát của phương trình ax + by = c (\(a \neq 0 \ hoặc\ b \neq 0\)) là: \(\left\{\begin{matrix}y=-\dfrac{a}{b}x+\dfrac{c}{d}\\ x \in R\end{matrix}\right.\)
- Nghiệm chung của hai phương trình là tọa độ giao điểm của hai đường thẳng.
Giải:
a) Nghiệm tổng quát của phương trình 2x + y = 4 là: \(\left\{\begin{matrix}y=-2x+4\\ x \in R\end{matrix}\right.\)
Nghiệm tổng quát của phương trình 3x + 2y = 5 là: \(\left\{\begin{matrix}y=-\dfrac{3}{2}x+\dfrac{5}{2}\\ x \in R\end{matrix}\right.\)
b) Đường thẳng biểu diễn tập nghiệm của phương trình: y = -2x + 4.
Cho x = 0 thì y = 4, ta xác định được điểm A(0; 4).
Cho y = 0 thì x = 2, ta xác định được điểm B(2; 0).
Vẽ đường thẳng biểu diễn tập nghiệm của phương trình: \(y=-\dfrac{3}{2}x+\dfrac{5}{2}.\)
Cho x = 0 thì \(y=\dfrac{5}{2}\). ta xác định được điểm C\((0;\dfrac{5}{2}).\)
Cho y = 0 thì \(x=\dfrac{5}{3}\), ta xác định được điểm \(B(\dfrac{5}{3};0).\)
Vẽ đường thẳng CD.
Nghiệm chung của hai phương trình là (3; -2).
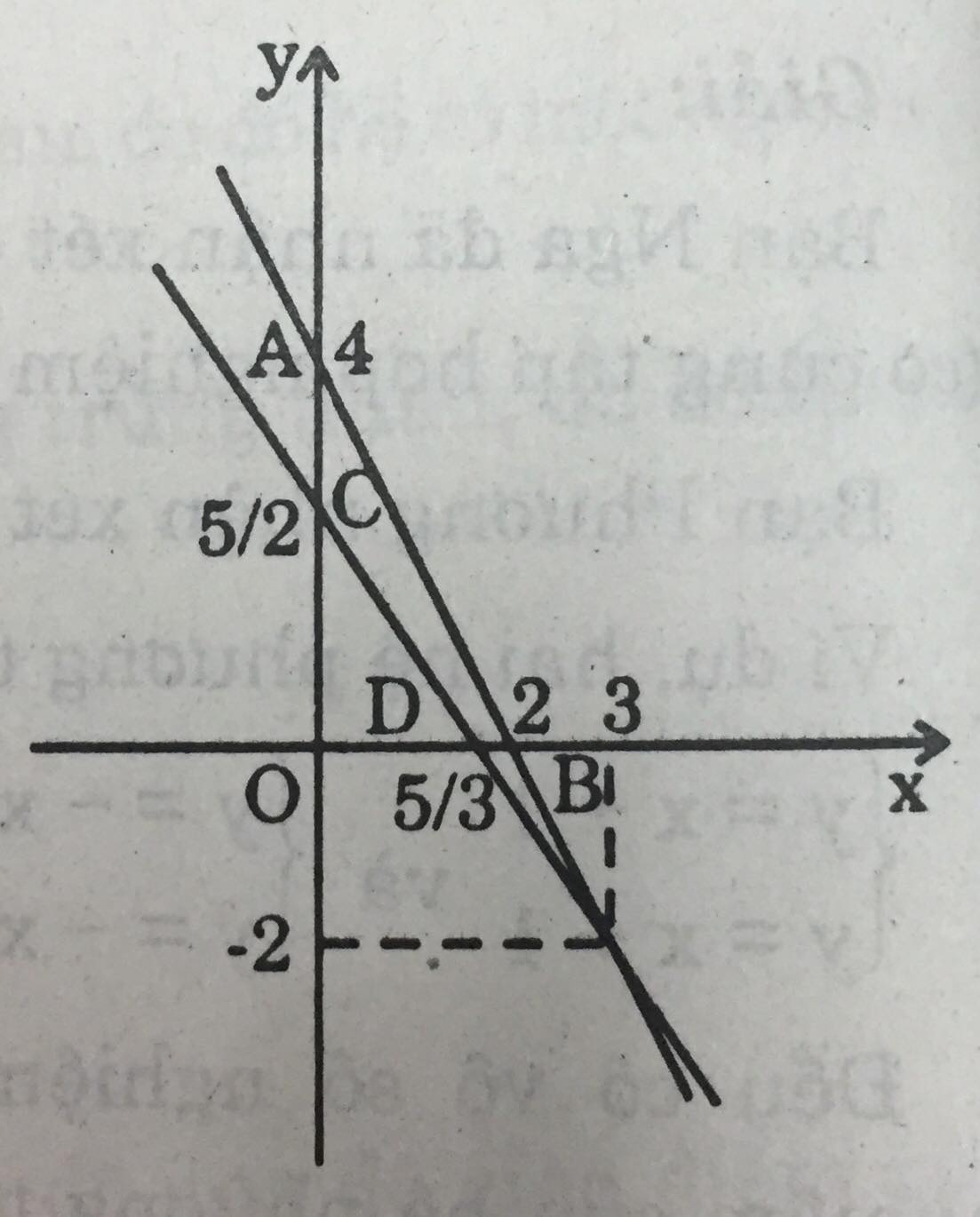
Copyright © 2021 HOCTAP247
