Giải bài 21 trang 19 - Sách giáo khoa Toán 9 tập 2

Đề bài

Giải các hệ phương trình sau bằng phương pháp cộng đại số:

Hướng dẫn giải

    a) Nhân hai vế của phương trình thứ nhất với \(- \sqrt{2} \), rồi cộng vế của hai phương trình của hệ ta có:

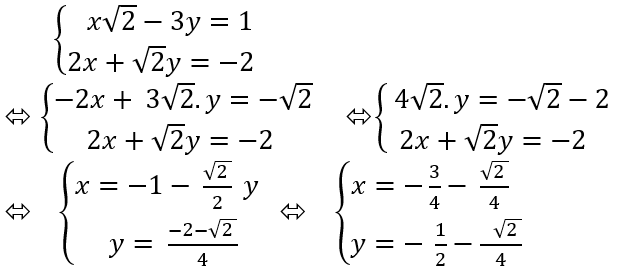
 Vậy hệ phương trình có nghiệm duy nhất ( \( - \dfrac{3}{4}+ \dfrac{\sqrt{2}}{8}; - \dfrac{1}{4}- \dfrac{\sqrt{2}}{4}\))

 b) Nhân hai vế của phương trình với \(\sqrt{2}\) rồi cộng từng vế hai phương trình của hệ ta có:

  \(\left\{\begin{matrix} & 5x \sqrt{3}+y = 2 \sqrt{2} \\ & x \sqrt{6}- y \sqrt{2}= 2 \end{matrix}\right. \Leftrightarrow\)\(\left\{\begin{matrix} & 5x \sqrt{3}+ x \sqrt{6} = 6 \sqrt{2} \\ & x \sqrt{6}- y \sqrt{2}= 2 \end{matrix}\right. \Leftrightarrow\) \(\left\{\begin{matrix} &x= \dfrac{1}{\sqrt{6}} \\ & x \sqrt{6}- y \sqrt{2}= 2 \end{matrix}\right. \Leftrightarrow\)\(\left\{\begin{matrix} &x= \dfrac{1}{\sqrt{6}} \\ & y =- \dfrac{1}{\sqrt{2}}\end{matrix}\right. \)

   Hệ có nghiệm duy nhất (\( \dfrac{1}{\sqrt{6}} , - \dfrac{1}{\sqrt{2}}\))