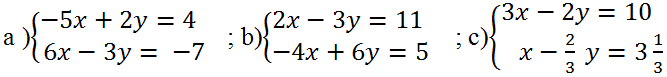Giải bài 22 trang 19 - Sách giáo khoa Toán 9 tập 2

Đề bài

 Giải các hệ phương trình sau bằng phương pháp cộng đại số:

Hướng dẫn giải

   Giải: 

  a) \(\left\{\begin{matrix} & -5x+ 2y = 4 \\ & 6x - 3y = -7\end{matrix}\right.\Leftrightarrow \)\(\left\{\begin{matrix} & -15x+ 6y = 12 \\ & 12x - 6y = -14\end{matrix}\right.\Leftrightarrow \)\(\left\{\begin{matrix} & -15x+ 6y = 12 \\ & - 3x = -2\end{matrix}\right.\Leftrightarrow \)

   \(\left\{\begin{matrix} & x= \dfrac{2}{3} \\ & y = \dfrac{11}{3}\end{matrix}\right. \)

   Hệ có nghiệm duy nhất ( \( x= \dfrac{2}{3}, y = \dfrac{11}{3}\)

    b) \(\left\{\begin{matrix} & 3x- 2y = 11 \\ & -4x+6y = 5\end{matrix}\right.\Leftrightarrow \)\(\left\{\begin{matrix} & 4x-6y =22 \\ & -4x + 6y = 5\end{matrix}\right.\Leftrightarrow \)\(\left\{\begin{matrix} & 4x-6y = 22 \\ & 0x + 0y = 27\end{matrix}\right. \)

   Hệ vô nghiệm.

   c) \(\left\{\begin{matrix} & 3x- 2y = 4 \\ & x- \dfrac{2}{3}y =3\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow \)\( \left\{\begin{matrix} & 3x- 2y = 10 \\ & 3x- 2y = 10\end{matrix}\right. \Leftrightarrow\) 3x- 2y = 10       \(\Leftrightarrow y = \dfrac{3}{2}x-5\)

   Hệ có vô số nghiệm với công thức: \(\left\{\begin{matrix} &y = \dfrac{3}{2}x-5 \\ & x \in R\end{matrix}\right.\)