Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Bài 3. Góc nội tiếp
Đề kiểm 15 phút - Đề số 3 - Bài 3 - Chương 3 - Hình học 9
Đề kiểm 15 phút - Đề số 3 - Bài 3 - Chương 3 - Hình học 9
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Từ một điểm P nằm ngoài đường tròn (O; R), kẻ hai tiếp tuyến PA, PB đến (O) ( A, B là hai tiếp điểm). Trên dây AB lấy M bất kì. Qua M kẻ đường vuông góc với OM cắt PA tại S và PB tại Q. Chứng minh rằng: \(MS = MQ\).
Hướng dẫn giải
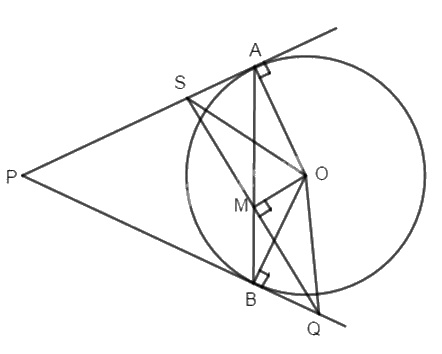
Ta có \(PA \bot OA\) hay \(SA \bot OA\) ( tính chất tiếp tuyến)
\(\Rightarrow \widehat {SAO} = 90^\circ \) nên A thuộc đường tròn đường kính SO.
\(OM \bot SQ\) (gt) \(\Rightarrow \widehat {SMO} = 90^\circ \)
Copyright © 2021 HOCTAP247
