Giải bài 23 trang 76 - Sách giáo khoa Toán 9 tập 2
Tóm tắt bài
Đề bài
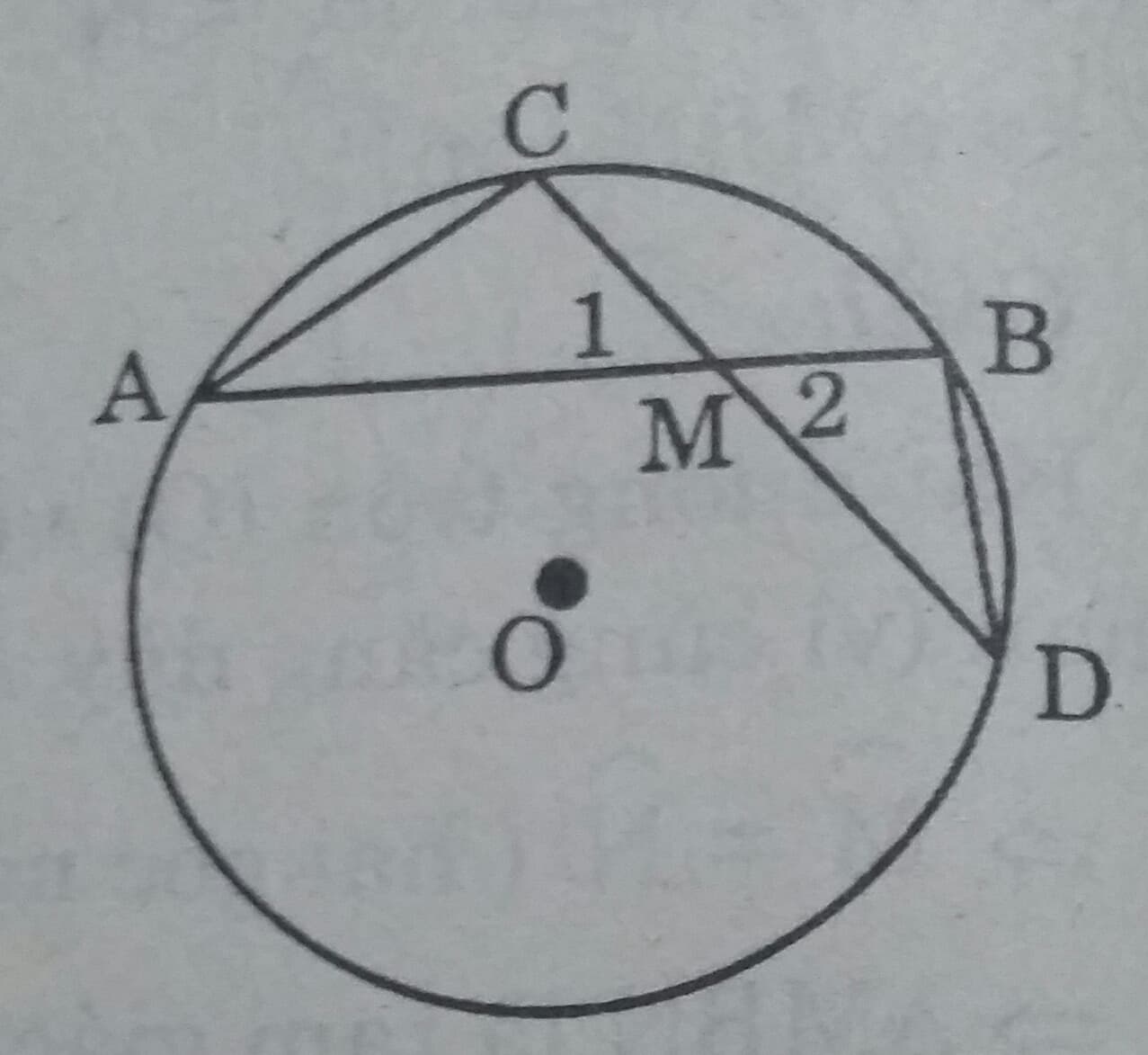
Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng . Đường thẳng thứ nhất cắt (O) tại A và B. Đường thẳng thứ hai cắt (O) tại C và D. Chứng minh MA.MB = MC.MD.
Hướng dẫn: Xét cả hai trường hợp điểm M nằm bên trong và bên ngoài đường tròn. Trong mỗi trường hợp, xét hai tam giác đồng dạng.
Hướng dẫn giải
Trường hợp M nằm bên trong đường tròn(h.29)
Xét \( \Delta MAC \ và \ \Delta MDB \) có:
\( \widehat{CAM}= \widehat{BDM}\) ( hai góc nội tiếp cùng chắn cung \(\stackrel\frown{BC}\))
\( \widehat{M_1}= \widehat{M_2}\) ( đối đỉnh)
Do đó \( \Delta MAC \approx \Delta MDB \)(g.g)
\( \Rightarrow \dfrac{MA}{MD}= \dfrac{MC}{MB}\Rightarrow MA.MB= MC.MD\)
Trường hợp điểm M nằm bên ngoài đường tròn: chứng minh tương tự.
Copyright © 2021 HOCTAP247
