Giải bài 19 trang 75 - Sách giáo khoa Toán 9 tập 2

Đề bài

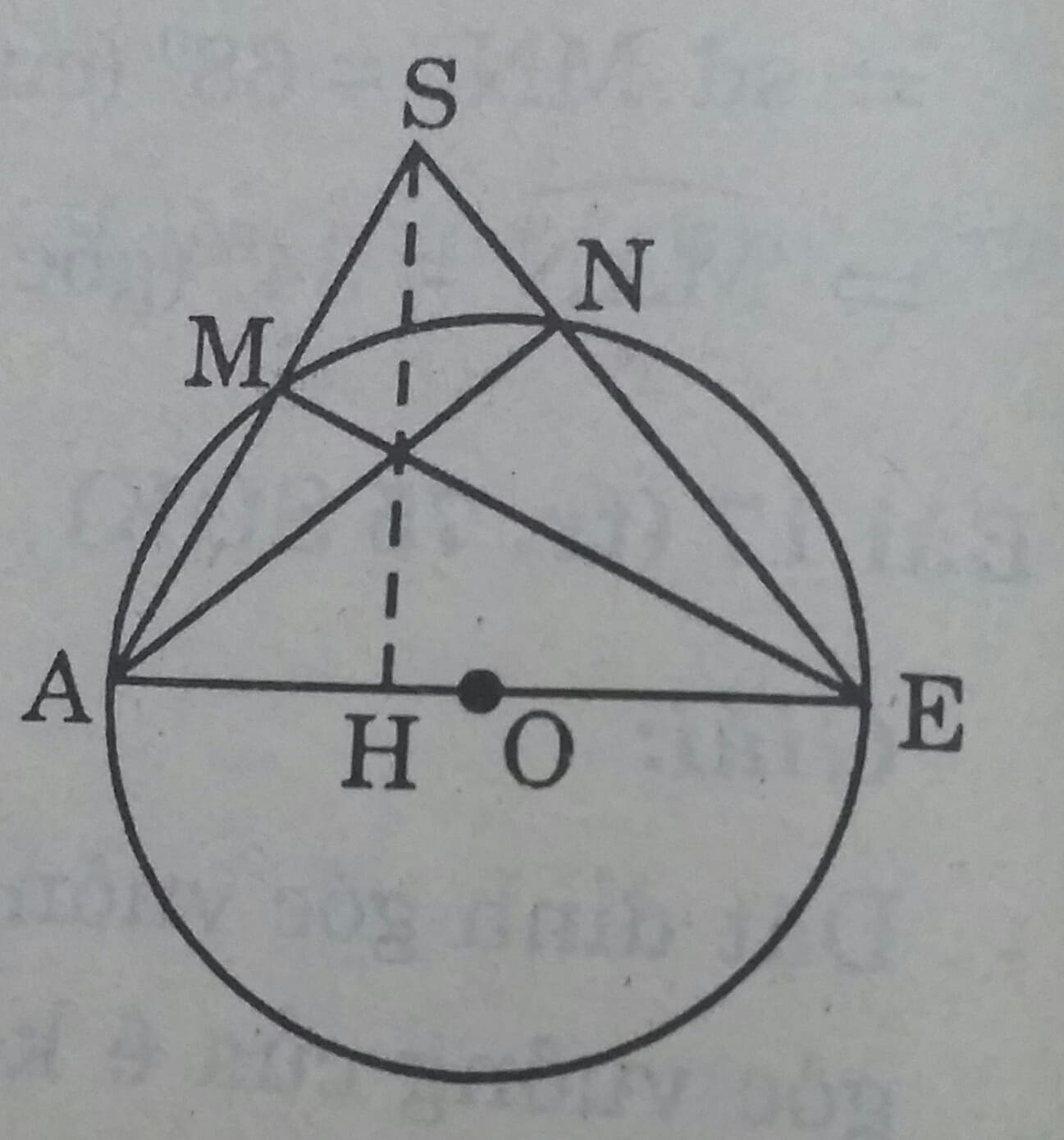
   Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.

Hướng dẫn giải

   Ta có \(\widehat{AMB}=\widehat{ANB}= 90^0\)( góc nội tiếp chắn nửa đường tròn đường kính AB) \(\Rightarrow AN \perp SB \ và\ BM \perp SA\)

   Do đó \(\Delta SAB \)  có hai đường cao AN và BM cắt nhau tại H \( \Rightarrow H \) là trực tâm  \(\Delta SAB \).

  \( ​​​​\Rightarrow SH \perp AB\)