Lý thuyết Góc nội tiếp đầy đủ nhất

Toán 9 góc nội tiếp là một trong những kiến thức trọng tâm khi nghiên cứu về Đường tròn. xin gửi tới các bạn lý thuyết bài giảng góc nội tiếp và các dạng bài tập góc nội tiếp lớp 9 chi tiết nhất. 

A. Một số lý thuyết cần nhớ về kiến thức của góc nội tiếp

1. Định nghĩa về góc nội tiếp

Trong phạm vi của một đường tròn, một góc được gọi là góc nội tiếp khi thỏa mãn được hai điều kiện sau đây:

- Đỉnh của góc nội tiếp thuộc đường tròn.

- Hai cạnh tạo nên góc là hai dây cung của đường tròn đó.

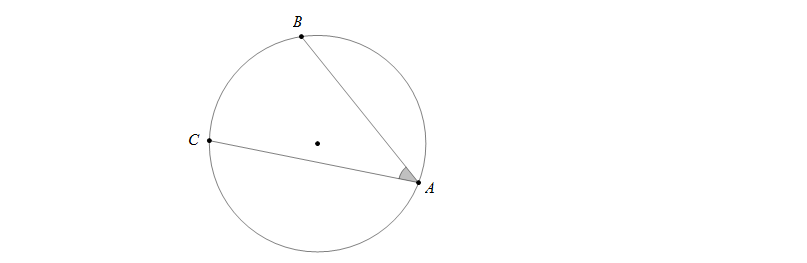
Bên trong góc nội tiếp chưa một cung, cung đó được gọi là cung bị chắn.

Ví dụ: góc nội tiếp là góc \(\widehat{BAC}\), cung bị chắn là cung \(\overbrace{BC}\)

2. Một số định lý về mối liên hệ giữa góc nội tiếp và cung bị chắn

Trong phạm vi một đường tròn, ta có định lý về mối liên hệ giữa góc nội tiếp và cung bị chắn như sau:

Số đo cung bị chắn gấp đôi số đo của góc nội tiếp hay nói cách khác là số đo góc nội tiếp bằng một nửa số đo cung bị chắn.

Ví dụ: \(\widehat{BAC}\) = \(\dfrac{1}{2}\)\(\overbrace{BC}\)

3. Một số hệ quả 

Trong phạm vi là một đường tròn, ta có những hệ quả sau được suy ra từ định nghĩa và tính chất của góc nội tiếp:

- Nếu hai góc nội tiếp có số đo bằng nhau thì hai góc nội tiếp đó chắn hai cung có số đo bằng nhau. Điều này cũng đúng trong trường hợp ngược lại, có nghĩa là nếu các cung bị chắn bởi các góc nội tiếp có số đo bằng nhau thì các góc nội tiếp đó có số đo bằng nhau.

- Nếu có một góc nội tiếp (điều kiện góc nội tiếp nhỏ hơn hoặc bằng \(90^0\)) và một góc ở tâm cùng chắn một cung thì ta có số đó góc nội tiếp bằng một nửa số đo góc ở tâm hay nói cách khác là số đo góc ở tâm gấp đôi số đo góc nội tiếp.

- Góc nội tiếp mà chắn nửa đường tròn thì có số đo bằng \(90^0\) (góc vuông)

B. Bài tập góc nội tiếp lớp 9

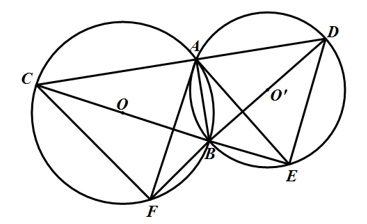
Bài 1: Gọi hai điểm A và B là giao điểm cắt của hai đường tròn tâm O bán kính R và đường tròn tâm O' bán kính R'. Cát tuyến \(CAD\) tạo với đường thẳng \(AB\) một góc bằng \(90^0\). Gọi E và F lần lượt là các điểm giao cắt của CB với đường tròn tâm O' và BD với đường tròn tâm O. Hãy làm sáng tỏ các nhận định sau:

\(a,\widehat{CAF}\) = \(\widehat{DAE}\)

b, Góc \(\widehat{FAE}\) nhận đường thẳng AB là tia phân giác

\(c, CA.CD\) = \(CB.CE\) 

\(d, CD^2\) = \(CB.CE\) + \(BD.CF\)

Hướng dẫn giải bài tập bài 1: 

Vì theo giả thiết cát tuyến \(CAD\) tạo với đường thẳng \(AB\) một góc bằng \(90^0\) 

=> \(CD\) \(\perp \) \(AB\) => \(\widehat{CAB}\) = \(90^0\)

Mà theo tính chất của góc nội tiếp ta có \(\widehat{CAB}\) = \(\dfrac{1}{2}\)\(\overbrace{BC}\) => sđ\(\overbrace{BC}\) = \(180^0\)

=> B, O, C thẳng hàng.

Chứng minh theo một cách tương tự ta có B, O', D cũng thẳng hàng.

a, Xét trong đường tròn tâm O bán kính R ta có: 

\(\widehat{CAF}\) = \(\widehat{CBF}\) (cùng chắn cung \(\overbrace{CF}\) nên có số đo bằng một nửa cung \(\overbrace{CF}\))

Xét trong (O'; R')

\(\widehat{DAE}\) = \(\widehat{DBE}\) (cùng chắn cung \(\overbrace{DE}\) nên có số đo bằng một nửa cung \(\overbrace{DE}\))

Mà \(\widehat{CBF}\) = \(\widehat{DBE}\) (tính chất của hai góc đối đỉnh) => \(\widehat{CAF}\) = \(\widehat{DAE}\) (điều phải chứng minh)

b, Vẽ hai dây cung \(CF\) thuộc đường tròn tâm O và \(DE\) thuộc đường tròn tâm O'.

Xét trong đường tròn tâm O bán kính R có:  \(\widehat{CFB}\) = \(90^0\) (tính chất góc nội tiếp chắn một nửa đường tròn)

Xét trong đường tròn tâm O' bán kính R' có:  \(\widehat{BED}\) = \(90^0\) (tính chất góc nội tiếp chắn một nửa đường tròn)

Xét hai tam giác là \(CFB\) và tam giác \(DEB\) ta có:

\(\widehat{CFB}\) = \(\widehat{BED}\) = \(90^0\)

\(\widehat{CBF}\) = \(\widehat{DBE}\) (tính chất của hai góc đối đỉnh)

=> \(\Delta \)\(CFB\) = \(\Delta \)\(DEB\) (theo trường hợp góc - góc) => \(\widehat{FCB}\) = \(\widehat{EDB}\)

Mặt khác, trong đường tròn tâm O bán kính R: 

\(\widehat{FAB}\) = \(\widehat{FCB}\) (cùng chắn cung \(\overbrace{FB}\) nên có số đo bằng một nửa cung \(\overbrace{FB}\))

Trong (O'; R')

\(\widehat{EAB}\) = \(\widehat{EDB}\) (cùng chắn cung \(\overbrace{EB}\) nên có số đo bằng một nửa cung \(\overbrace{EB}\))

=> \(\widehat{FAB}\) = \(\widehat{EAB}\) => Góc \(\widehat{FAE}\) nhận đường thẳng AB là tia phân giác (điều phải chứng minh)

c, Xét hai tam giác là \(CAE\) và tam giác \(CBD\) ta có:

Góc \(\widehat{C}\) chung

\(\widehat{CEA}\) = \(\widehat{BDA}\) (cùng chắn cung \(\overbrace{AB}\) nên có số đo bằng một nửa cung \(\overbrace{AB}\))

=> \(\Delta \)\(CAE\) \(\sim\) \(\Delta \)\(CBD\) (theo trường hợp góc - góc) => \(\dfrac{CA}{CB}\) = \(\dfrac{CE}{CD}\)

=> \(CA.CD\) = \(CB.CE\) (điều phải chứng minh) (1)

d, Xét hai tam giác là \(DAF\) và tam giác \(DBC\) ta có:

Góc \(\widehat{D}\) chung

\(\widehat{DFA}\) = \(\widehat{DCB}\) (cùng chắn cung \(\overbrace{AB}\) nên có số đo bằng một nửa cung \(\overbrace{AB}\))

=> \(\Delta \)\(DFA\) \(\sim\) \(\Delta \)\(DCB\) (theo trường hợp góc - góc) => \(\dfrac{DA}{DB}\) = \(\dfrac{DF}{DC}\)

=> \(DA.DC\) = \(DB.DF\) (2)

Từ (1) và (2) => \(DA.DC\) + \(CA.CD\) = \(DB.DF\) + \(CB.CE\)

<=> \(DC(DA+CA)\) = \(DB.DF\) + \(CB.CE\)

<=> \(CD^2\) = \(DB.DF\) + \(CB.CE\) (điều phải chứng minh)

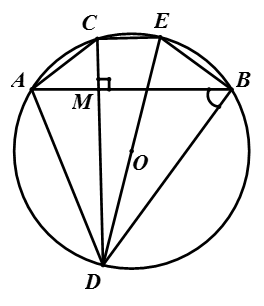
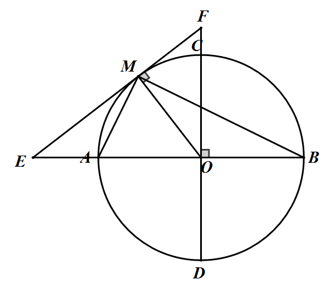
Bài 2: Cho một điểm M nằm bên trong mặt phẳng của đường tròn tâm O bán kính R. Xuất phát từ điểm M, kẻ hai dây cung \(AB\) và \(CD\) sao cho hai dây cung này tạo với nhau một góc bằng \(90^0\) (điểm C nằm trên cung nhỏ AB). Đường kính \(DE\) đi qua tâm O. Hãy sáng tỏ một số nhận định sau:

\(a, MA.MB\) = \(MC.MD\)

b, Tứ giác ABEC có dạng là một hình thang cân.

c, Một tổng \(AD^2+BC^2\) có độ lớn không thay đổi khi điểm M dịch chuyển trong mặt phẳng của đường tròn tâm O bán kính R.

Hướng dẫn giải bài tập bài 2:

a, Xét hai tam giác là \(AMC\) và tam giác \(DMB\) ta có:

\(\widehat{AMC}\) = \(\widehat{BMD}\) = \(90^0\)

\(\widehat{ACD}\) = \(\widehat{ABD}\) (cùng chắn cung \(\overbrace{AD}\) nên có số đo bằng một nửa cung \(\overbrace{AD}\))

=> \(\Delta \)\(AMC\) \(\sim\) \(\Delta \)\(DMB\) => \(\dfrac{MA}{MD}\) = \(\dfrac{MC}{MB}\)

=> \(MA.MB\) = \(MC.MD\) (điều phải chứng minh)

b, Xét trong đường tròn tâm O bán kính R:

\(\widehat{DCE}\) = \(90^0\) => \(CD\) \(\perp \) \(CE\) 

Mà  \(CD\) \(\perp \) \(AB\) (theo giả thiết đề bài) => \(AB//CE\)

=> ABEC là hình thang

Mặt khác ta lại có \(CE//AB\) => \(\overbrace{AC}\) = \(\overbrace{BE}\) => \(\overbrace{AE}\) = \(\overbrace{BC}\) => \(\widehat{ABE}\) = \(\widehat{BAC}\)

=> ABEC là một hình thang cân.

c, Theo kết quả của ý b, \(\overbrace{AE}\) = \(\overbrace{BC}\) => \(EB=BC\) 

Xét trong đường tròn tâm O bán kính R có

\(\widehat{DAE}\) = \(90^0\) 

=> \(MA^2\) + \(MB^2\) + \(MC^2\) + \(MD^2\) = (\(MA^2\) + \(MD^2\)) + (\(MB^2\) + \(MC^2\))

= \(AD^2+BC^2\) = \(DE^2\) = \(R^2\) (luôn cố định)

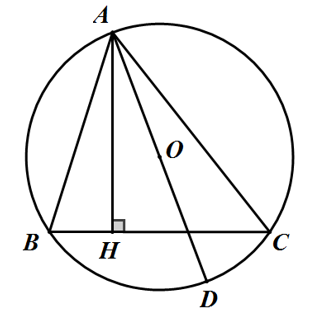
Bài 3: Cho đường tròn tâm O bán kính R ngoại tiếp một tam giác \(ABC\). Xuất phát từ điểm A, kẻ một đường thẳng \(AH\) sao cho đường thẳng \(AH\) tạo với \(BC\) một góc  bằng \(90^0\), D là giao điểm cắt của \(AO\) và (O; R). Hãy sáng tỏ các nhận định sau: 

\(a,\Delta ABH\) = \(\Delta ADC\)

\(b,S=\dfrac{abc}{4R}\) với S là ký hiệu của diện tích tam giác \(ABC\) và a, b, c lần lượt là ba cạnh của tam giác.

Hướng dẫn giải bài tập bài 3:

a, Xét hai tam giác là \(ABH\) và tam giác \(ADC\) ta có:

\(\widehat{AHB}\) = \(\widehat{ACD}\) = \(90^0\)

\(\widehat{ABC}\) = \(\widehat{ADC}\) (cùng chắn cung \(\overbrace{AC}\) nên có số đo bằng một nửa cung \(\overbrace{AC}\))

=> \(\Delta \)\(ABH\) \(\sim\) \(\Delta \)\(ADC\) (theo trường hợp góc - góc)

b, Ta có \(\Delta \)\(ABH\) \(\sim\) \(\Delta \)\(ADC\) (theo trường hợp góc - góc)

=>  \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AC}\) => \(AH\) = \(\dfrac{AB.AC}{AD}\) = \(\dfrac{bc}{2R}\)

Công thức tính diện tích tam giác \(ABC\) là: \(S=\) \(\dfrac{1}{2}\)\(AH.BC\) = \(\dfrac{1}{2}\). \(\dfrac{bc}{2R}\).a = \(\dfrac{abc}{4R}\) (điều phải chứng minh)

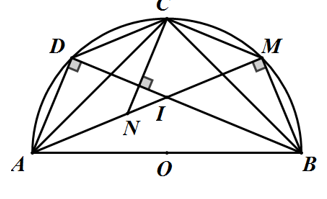
Bài 4: Gọi AB là đường kính của đường tròn tâm O bán kính R và trên cung AB lấy một điểm C sao cho C là điểm chính giữa của cung AB. Trên cung BC và tia AM lần lượt lấy hai điểm là M và N thỏa mãn điều kiện là AN = BM. Xuất phát từ điểm C, kẻ một dây cung CD thỏa mãn điều kiện là \(CD//AM\).

a, Chứng minh nhận định \(\Delta ACN\) = \(\Delta BCM\)

b, Chứng minh nhận định \(\Delta CMN\) là một tam giác vuông cân 

c, Tứ giác ANCD có dạng hình gì? Giải thích lý do?

Hướng dẫn giải bài tập bài 4:

a, Xét hai tam giác là \(ABH\) và tam giác \(ADC\) ta có:

\(AC=BC\) (theo giả thiết đề bài có C là điểm chính giữa của cung AB)

\(\widehat{CAN}\) = \(\widehat{CBN}\) (cùng chắn cung \(\overbrace{CM}\) nên có số đo bằng một nửa cung \(\overbrace{CM}\))

\(AN=BM\) (theo dữ kiện đề bài)

=> \(\Delta \)\(ACN\) \(=\) \(\Delta \)\(BCM\) (theo trường hợp cạnh - góc - cạnh) (điều phải chứng minh)

b, Vì ta vừa chứng minh được theo ý a là \(\Delta \)\(ACN\) \(=\) \(\Delta \)\(BCM\) (theo trường hợp cạnh - góc - cạnh)

=> \(CN=CM\) => \(\Delta \)\(CMN\) cân tại C 

Lại có trong đường tròn tâm O bán kính R: \(\widehat{CMA}\) = \(\dfrac{1}{2}\)\(\overbrace{AC}\) = \(\dfrac{1}{2}\). \(90^0\) = \(45^0\)

=> \(\Delta \)\(CMN\) là một tam giác vuông cân tại C (điều phải chứng minh)

c, Đi từ giả thiết đề bài \(CD//AM\) => ADCN có dạng là một hình thang cân

Ta lại có theo kết quả của ý b, \(\widehat{DAM}\) = \(\widehat{CMN}\) = \(\widehat{CNM}\) = \(45^0\)

=> \(AD//CN\) => Tứ giác ADCN là một hình bình hành (điều phải chứng minh)

Bài 5: Trong đường tròn tâm O bán kính R lần lượt cho AB và CD là hai đường kính của đường tròn thỏa mãn điều kiện là AB tạo với CD một góc bằng \(90^0\). Trên cung nhỏ AC lấy bất kỳ một điểm M không trùng với A và E. Kẻ một tiếp tuyến thỏa mãn M là tiếp điểm của đường tròn, tiếp tuyến này lần lượt cắt AB và CD kéo dài tại E và F.

a, Chứng minh nhận định \(\widehat{MFO}\) = 2\(\widehat{MBO}\)

b, Giả sử muốn \(\widehat{FEO}\) = \(30^0\) thì điểm M nằm tại vị trí nào trên cung nhỏ AC. Trong trường hợp đó, xác định độ dài đoạn thẳng OE, ME, EF dựa theo R.

Hướng dẫn giải bài tập bài 5: 

a, Theo giả thiết ta có \(\widehat{MOA}\) = 2\(\widehat{MBO}\) (vì \(\widehat{MOA}\) là góc ở tâm và \(\widehat{MBO}\) là góc nội tiếp cùng chắn một cung \(\overbrace{AM}\))

Ta có \(\widehat{MOA}\) = \(\widehat{EFO}\) (vì cùng bằng \(90^0\) - \(\widehat{FEO}\))

=> \(\widehat{EFO}\) = 2\(\widehat{MBO}\) (điều phải chứng minh)

b, Theo giả thiết của đề bài \(\widehat{FEO}\) = \(30^0\) => \(\widehat{MOA}\) = \(90^0\) - \(\widehat{FEO}\) = \(90^0\) - \(30^0\) = \(60^0\)

\(\Delta \)\(AOM\) là một tam giác cân tại O vì \(OM=OA=R\) mà \(\widehat{MOA}\) = \(60^0\)

=> \(\Delta \)\(AOM\) là một tam giác đều => \(AM = R\)

Giả sử M thuộc vào đường tròn tâm O bán kính R và \(AM = R\) thì \(\widehat{FEO}\) = \(30^0\)

Xét trong tam giác OME có \(\widehat{OME}\) = \(180^0\) - \(\widehat{OEM}\) - \(\widehat{EOM}\) = \(180^0\) - \(30^0\) - \(60^0\) = \(90^0\)

=> Vậy \(OME\) vuông tại M. Sử dụng công thức tỉ số lượng giác trong tam giác vuông ta có:

\(ME\) = \(OM\). tan\(\widehat{MOA}\) = \(R\sqrt{3}\) 

\(OE\) = \(2MO\) = \(2R\)

Vì \(\Delta \)\(EOF\) có \(\widehat{O}\) = \(90^0\) nên áp dụng công thức tỉ số lượng giác trong tam giác vuông có:

cos\(\widehat{FEO}\) = \(\dfrac{EO}{EF}\) => \(EF\) = \(\dfrac{EO}{cos\widehat{FEO}}\) = \(\dfrac{2R}{cos30^0}\) = \(\dfrac{4R\sqrt{3}}{3}\)

Tham khảo thêm >>> Giải bài tập toán 9 góc nội tiếp

đã gửi đến các bạn bài góc nội tiếp lớp 9 và các dạng bài tập góc nội tiếp lớp 9 thông qua bài viết toán 9 góc nội tiếp. Nếu có đóng góp gì cho bài viết góc nội tiếp, các bạn hãy để lại comment dưới phần bình luận nhé!