Giải bài 25 trang 76 - Sách giáo khoa Toán 9 tập 2
Tóm tắt bài
Đề bài
Dựng một tam giác vuông, biết cạnh huyền dài 4cm và một cạnh góc vuông dài 2,5cm.
Hướng dẫn giải
Phân tích: Giả sử dựng được \(\Delta ABC\) thỏa mãn yêu cầu bài toán, khi đó \(\Delta ABC\) phải thỏa mãn hai điều kiện:
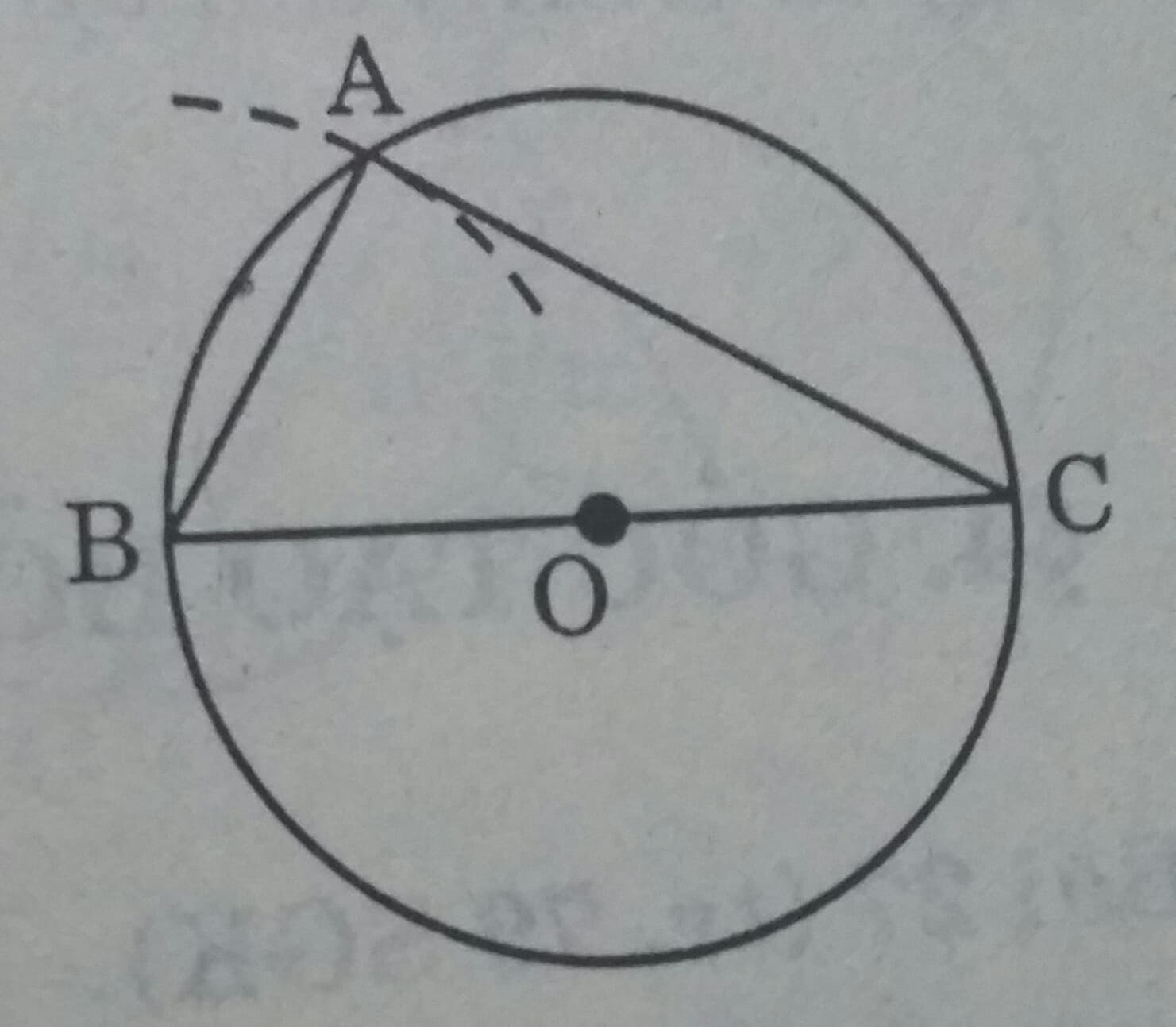
BC là đường kính của đường tròn đi qua điểm A
Cung tròn (B;2,5cm) đi qua điểm A;
Điểm A là giao điểm của đường tròn (O) và cung tròn (B;2,5) và \(\Delta ABC\) là tam giác phải dựng.
Cách dựng:
Dựng đường tròn (O) đường kính BC = 4cm
Dựng cung tròn (B;2,5 cm) cắt đường tròn (O) tại điểm A.
Nối AB, AC ta được \(\Delta ABC\) phải dựng.
Chứng minh:
Ta có AB là bán kính cung tròn (B; 2,5cm) \(\Rightarrow \) AB = 2,5cm.
\(\widehat{BAC}= 90^0\) ( nội tiếp chắn nửa đường tròn đường kính BC)
Vậy \(\Delta ABC\) vuông tại A có BC = 4cm và AB= 2,5cm.
Copyright © 2021 HOCTAP247
