Đề kiểm 15 phút - Đề số 6 - Bài 5 - Chương 3 - Hình học 9
Tóm tắt bài
Đề bài
Tam giác ABC đều nội tiếp trong đường tròn (O), D là một điểm trên cung BC. Các đường thẳng AB và CD cắt nhau tại E, AC và BD cắt nhau tại F. Chứng minh rằng: \(AB^2= BE.CF\).
Hướng dẫn giải
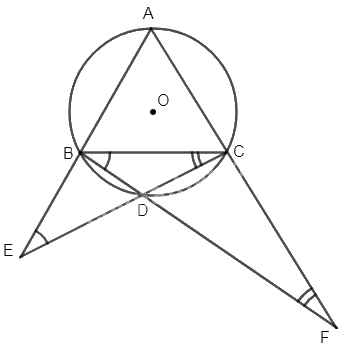
Ta có :
\(\widehat {BED} =\dfrac {{sd\overparen{AC} - sd\overparen{BD}}}{ 2} \)
\(\;\;\;\;\;\;\;\;\;\,= \dfrac{{sd\overparen{BC} - sd\overparen{BD}} }{ 2}\) (vì \(\overparen{AC} = \overparen{ BC}\))
\(\;\;\;\;\;\;\;\;\;\,=\dfrac{{sd\overparen{DC}} }{ 2}\) ( góc có đỉnh nằm ngoài đường tròn)
\(\widehat {CBF} = \dfrac{{sd\overparen{DC}}}{2}\) ( góc nội tiếp)
\(\Rightarrow \widehat {BED} = \widehat {CBF}\)
Tương tự ta chứng minh được \(\widehat {CFD} = \widehat {BCE}\).
Vậy \(∆BCE\) và \(∆CFB\) đồng dạng (g.g)
\( \Rightarrow \dfrac{{BC} }{ {CF}} =\dfrac {{BE}}{ {BC}}\)
\( \Rightarrow BC^2= BE.CF\) mà \(BC = AB\) (gt)
\( \Rightarrow AB^2= BE.CF.\)
Copyright © 2021 HOCTAP247
