Giải bài 40 trang 83 - Sách giáo khoa Toán 9 tập 2
Tóm tắt bài
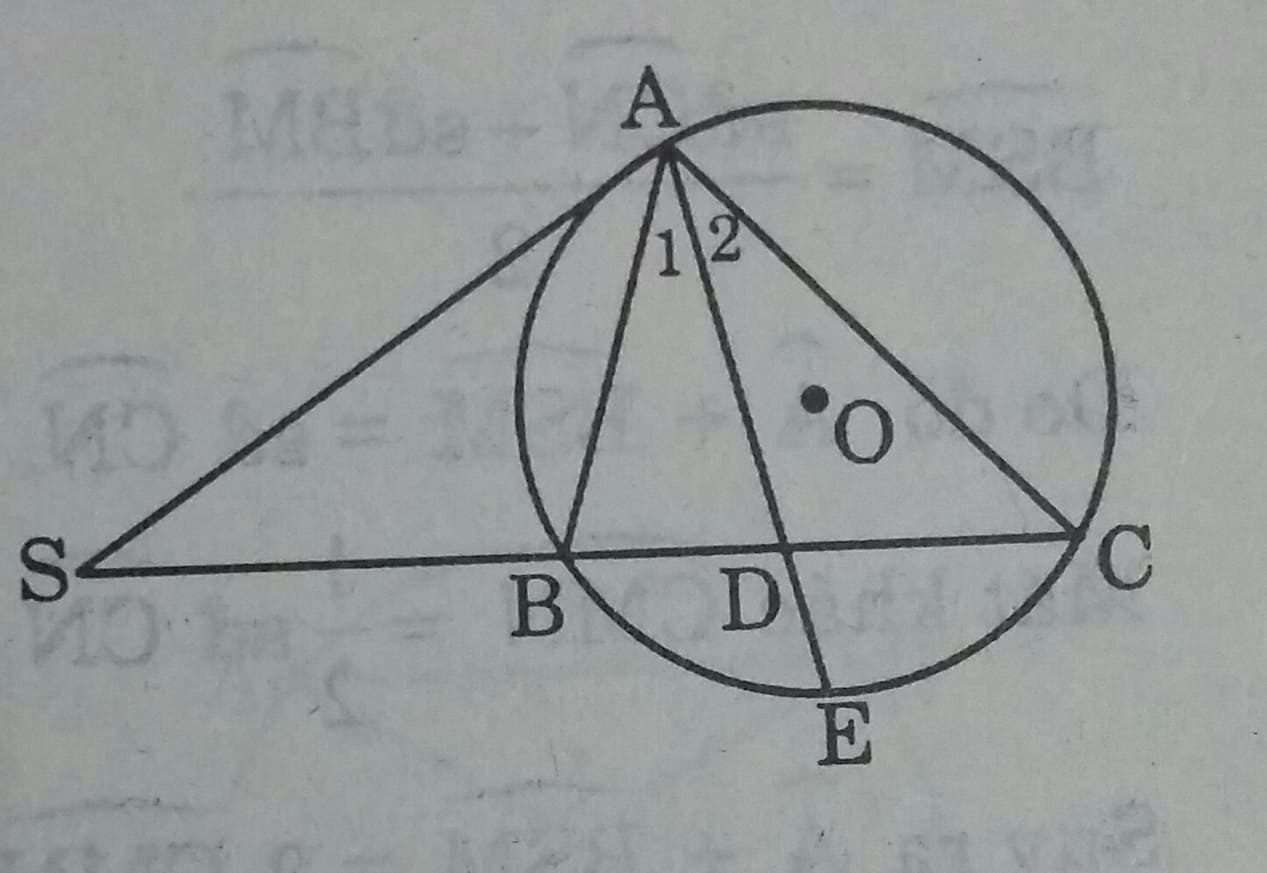
Đề bài
Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cắt cát tuyển SBC của đường tròn . Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.
Hướng dẫn giải
Gọi E là giao điểm của tia phân giác AD với đường tròn (O).
Vì \(\widehat{A_1}= \widehat{A_2} \ nên \ sđ \stackrel\frown{EB}=sđ \stackrel\frown{EC} \\ \widehat{SDA} \ là \ góc \ có \ đỉnh \ ở \ bên \ trong \ đường \ tròn \ nên: \widehat{SDA}= \dfrac{sđ \stackrel\frown{AB}+ sđ \stackrel\frown{CE}}{2}= \dfrac{sđ \stackrel\frown{AB}+ sđ \stackrel\frown{BE}}{2}= \dfrac{sđ \stackrel\frown{ABE}}{2}\) Góc \( \widehat{SDA}\) là góc tạo bởi tia tiếp tuyến và dây cung nên:
\( \widehat{SDA}= \dfrac{1}{2}sđ \stackrel\frown{ABE}\\ Suy \ ra \ \widehat{SDA}= \widehat{SAD} \Rightarrow \Delta SAD \ cân \Rightarrow SA= AD\)
Copyright © 2021 HOCTAP247
