Đề kiểm 15 phút - Đề số 9 - Bài 5 - Chương 3 - Hình học 9

Đề bài

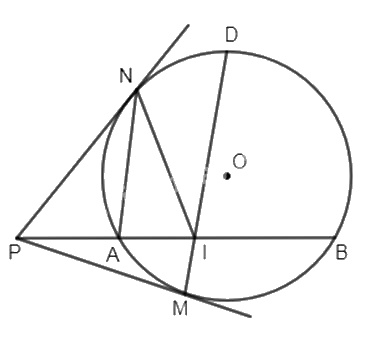
Cho đường  tròn (O). Từ điểm P bên ngoài đường tròn kẻ cát tuyến PAB và hai tiếp tuyến PM, PN với (O) (M thuộc cung nhỏ AB). Lấy D là điểm chính giữa của cung lớn AB, DM cắt AB tại I.

a)Chứng minh: \(PM = PI\).           

b) Chứng minh: \(IA.NB = IB.NA\)

Hướng dẫn giải

a) Ta có \(\widehat {PMD} = \dfrac{{sd\overparen{DA} + sd\overparen{MA}}}{ 2}\) ( góc giữa tiếp tuyến và một dây)

\(\widehat {PIM} = \dfrac{{sd\overparen{DB} + sd\overparen{MA}}}{ 2}\) ( góc có đỉnh bên trong đường tròn)

Mà \(\overparen{ DB} = \overparen{ DA}\) (gt) \( \Rightarrow \widehat {PMD} = \widehat {PIM}\)

Do đó \(∆PMI\) cân tại đỉnh P \( \Rightarrow PM = PI.\)

b) \(PM = PN\) ( (tính chất hai tiếp tuyến cắt nhau)

Mà \(PM = PI\) (cmt)  \( \Rightarrow PN = PI\) nên \(∆PNI\) cân \( \Rightarrow \widehat {PNI} = \widehat {PIN}\)

Mà \(\widehat {PNI} = \widehat {PNA} + \widehat {ANI}\) và \(\widehat {PIN} = \widehat {INB} + \widehat B\) ( góc ngoài của ∆NIB)

Mà \(\widehat B = \widehat {PNA}\) (góc nội tiếp bằng góc giữa tiếp tuyến và một dây)

\( \Rightarrow \widehat {ANI} = \widehat {INB}\) hay NI là phân giác của \(∆ANB.\)

Theo tính chất đường phân giác, ta có :

\(\dfrac{{IA}}{{IB}} = \dfrac{{NA} }{ {NB}}\)

\( \Rightarrow  IA.NB = IB.NA.\)