Giải bài 38 trang 38 - Sách giáo khoa Toán 9 tập 2
Tóm tắt bài
Đề bài
Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho
Hướng dẫn giải
a) Các góc \(\widehat{E}\ và \ \widehat{T}\) là các góc có đỉnh ở bên ngoài đường tròn.
\(\widehat{E}= \dfrac{sđ \stackrel\frown{AB}-sđ \stackrel\frown{CD}}{2} = \dfrac{180^0 - 160^0}{2}= 60^0 \\ \widehat{T}= \dfrac{ sđ \widehat{BDC} - sđ \widehat{BAC} }{2} = \dfrac{(180^0 +60^0)-(60^0+60^0)}{2}= 60^0 \\ Vậy \widehat{E}= \widehat{T} \ hay \ \widehat{AEB}= \widehat{BTC}\)
\(\widehat{DCT} \) là góc tạo bởi tia tiếp tuyến và dây cung nên:
\( \widehat{DCT}= \dfrac{1}{2} sđ \stackrel\frown{CD}= \dfrac{1}{2} .60^0 = 30^0\\ \widehat{DCB} \ là \ góc \ nội \ tiếp \ nên \widehat{DCB}= \dfrac{1}{2} sđ \stackrel\frown{BD}= \dfrac{1}{2} .60^0 = 30^0\\\)
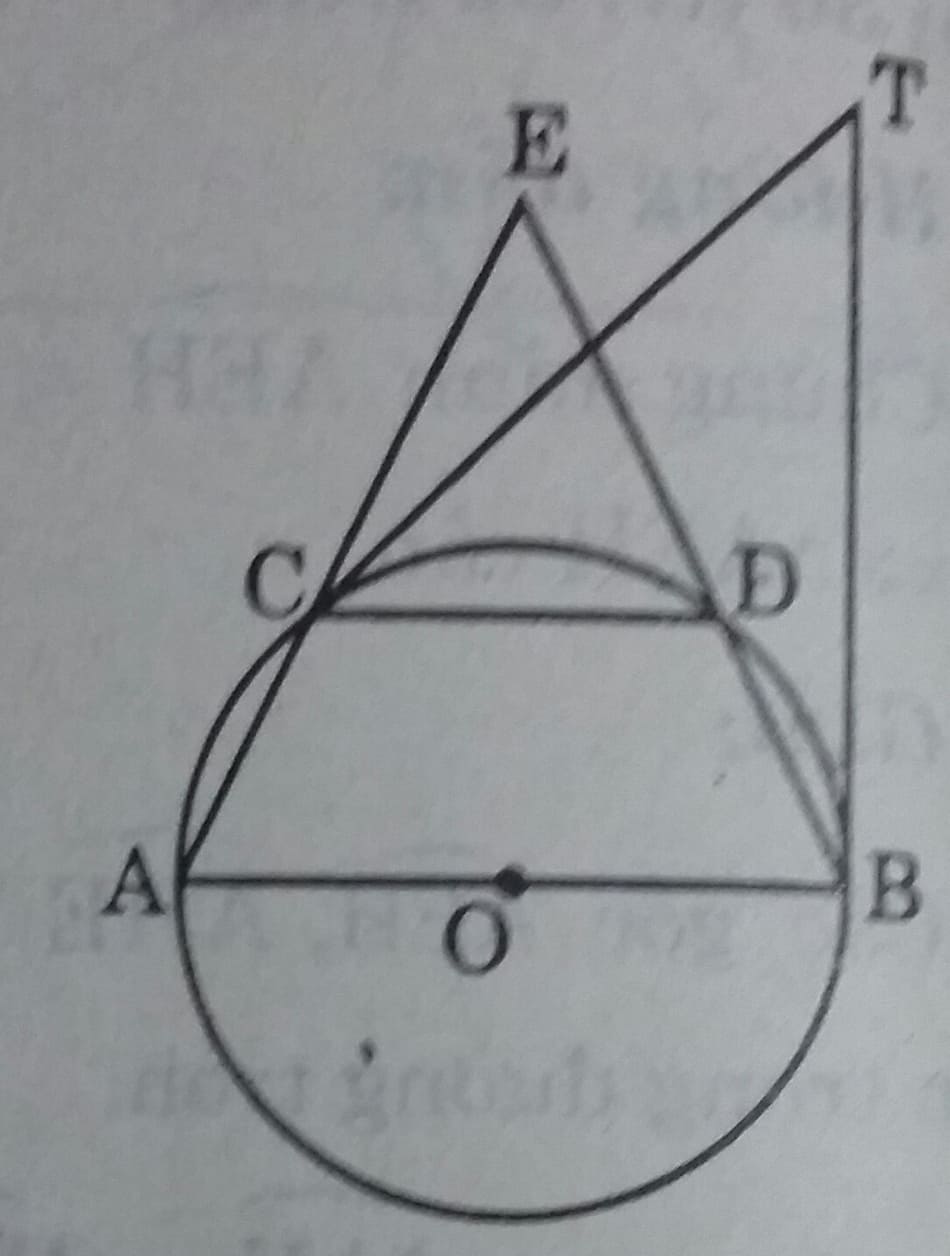
Copyright © 2021 HOCTAP247
