Giải bài 114 trang 50 - Sách giáo khoa Toán 9 tập 2
Tóm tắt bài
Đề bài
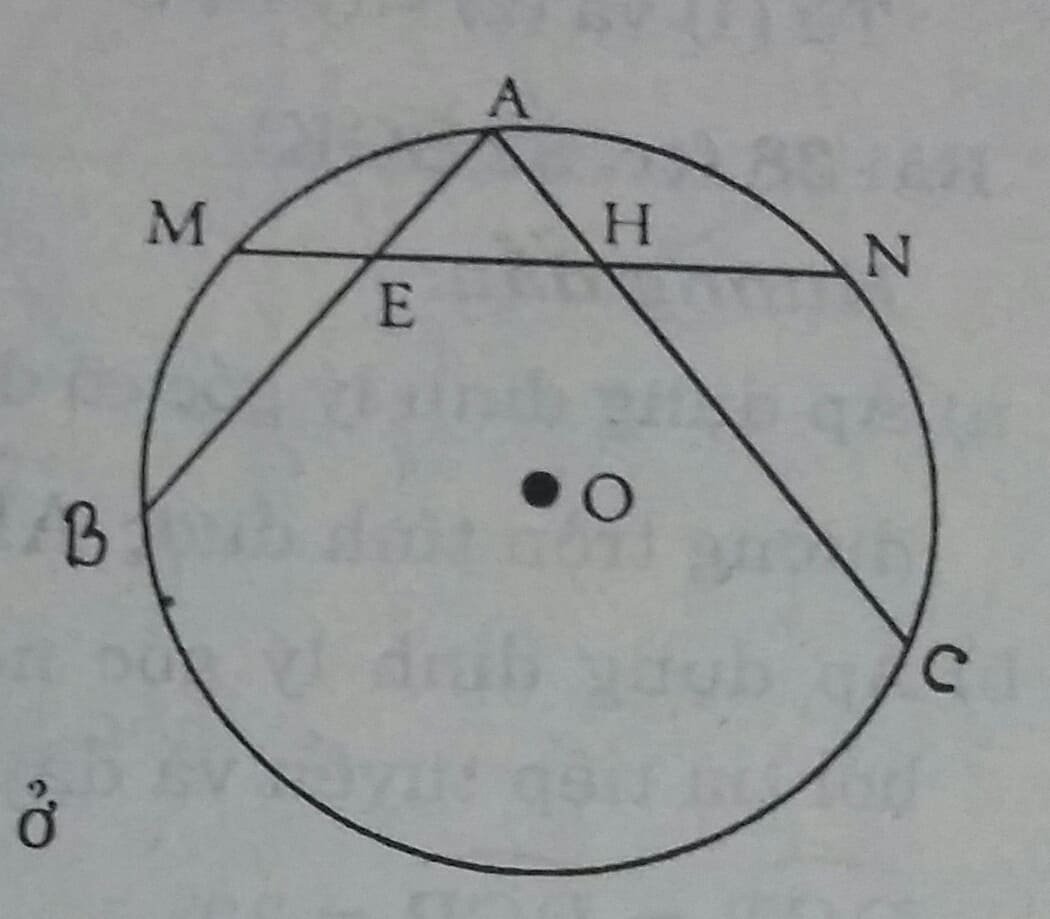
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
Hướng dẫn giải
Các góc \( \widehat{AEH},\widehat{AHE}\) là các góc có đỉnh ở bên trong đường tròn.
\( \widehat{AEH} = \dfrac{sđ \stackrel\frown{AN} +sđ \stackrel\frown{BM} }{2} = \dfrac{sđ \stackrel\frown{AN} +sđ \stackrel\frown{AM}}{2}= \dfrac{sđ \stackrel\frown{MAN}}{2} \ (1)\\\widehat{AHE} = \dfrac{sđ \stackrel\frown{AM} +sđ \stackrel\frown{CN}} {2} = \dfrac{sđ \stackrel\frown{AM} +sđ \stackrel\frown{CN} }{2}= \dfrac{sđ \stackrel\frown{MAN}}{2} \ (2)\\ Từ \ (1) \ và (2) \ suy\ ra \ \widehat{AEH}= \widehat{AHE} \Rightarrow \Delta AEH \ cân\)
Copyright © 2021 HOCTAP247
