Giải bài 43 trang 83 - Sách giáo khoa Toán 9 tập 2

Đề bài

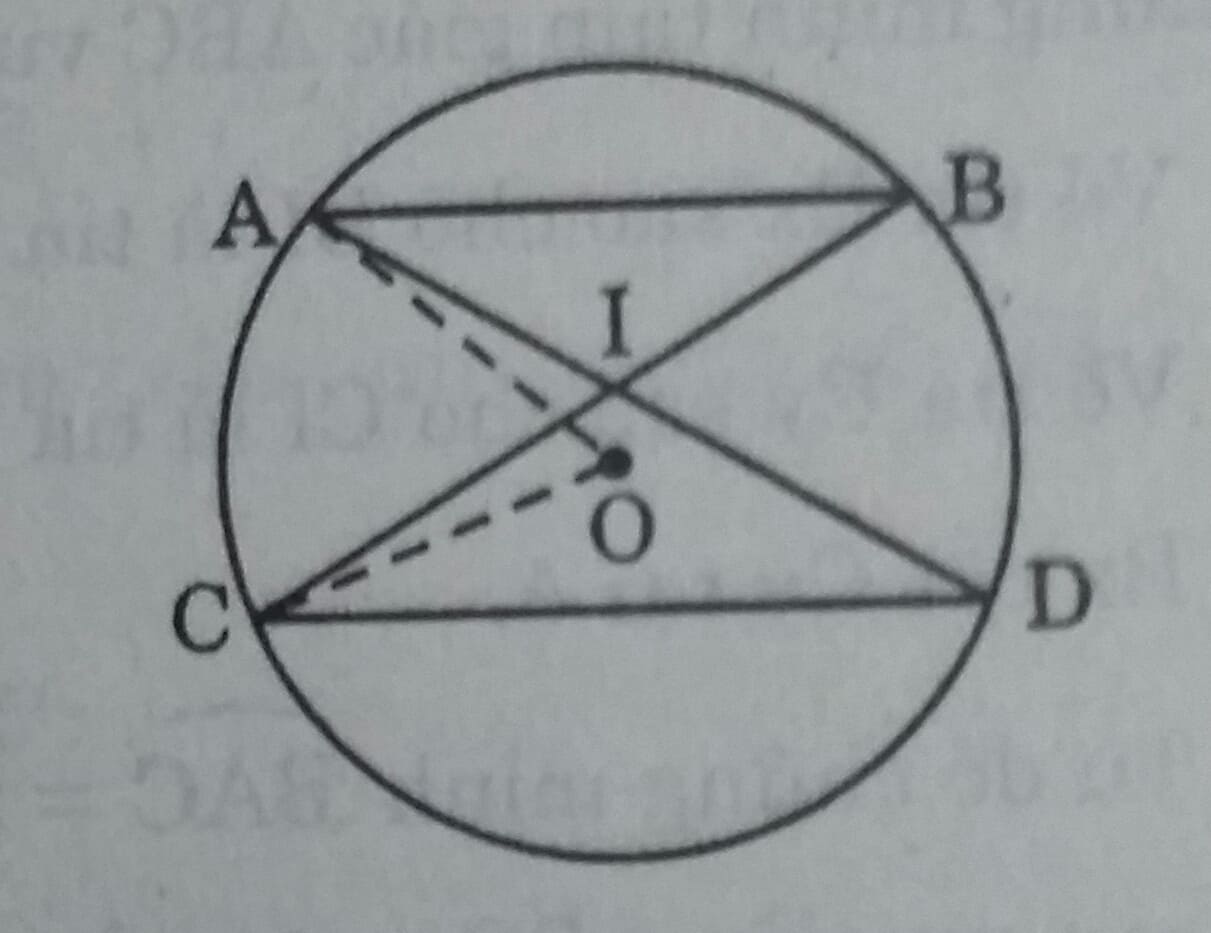
   Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I.

Hướng dẫn giải

    Ta có AB// CD nên \(\stackrel\frown{AC}=\stackrel\frown{BD}\)

    Góc \(\widehat{AIC}\) là góc có đỉnh ở bên trong đường tròn nên:

   \(\widehat{AIC}= \dfrac{\stackrel\frown{AC}+ \stackrel\frown{BD}}{2}= \dfrac{2sđ \stackrel\frown{BD}}{2}= sđ \stackrel\frown{AC}\\ Góc \ \widehat{AOC}\ là \ góc \ ở \ tâm \ nên: \widehat{AOC}= sđ \stackrel\frown{AC}\\ Suy \ ra \widehat{AIC}= \widehat{AOC}\)