Giải bài 41 trang 83 - Sách giáo khoa Toán 9 tập 2

Đề bài

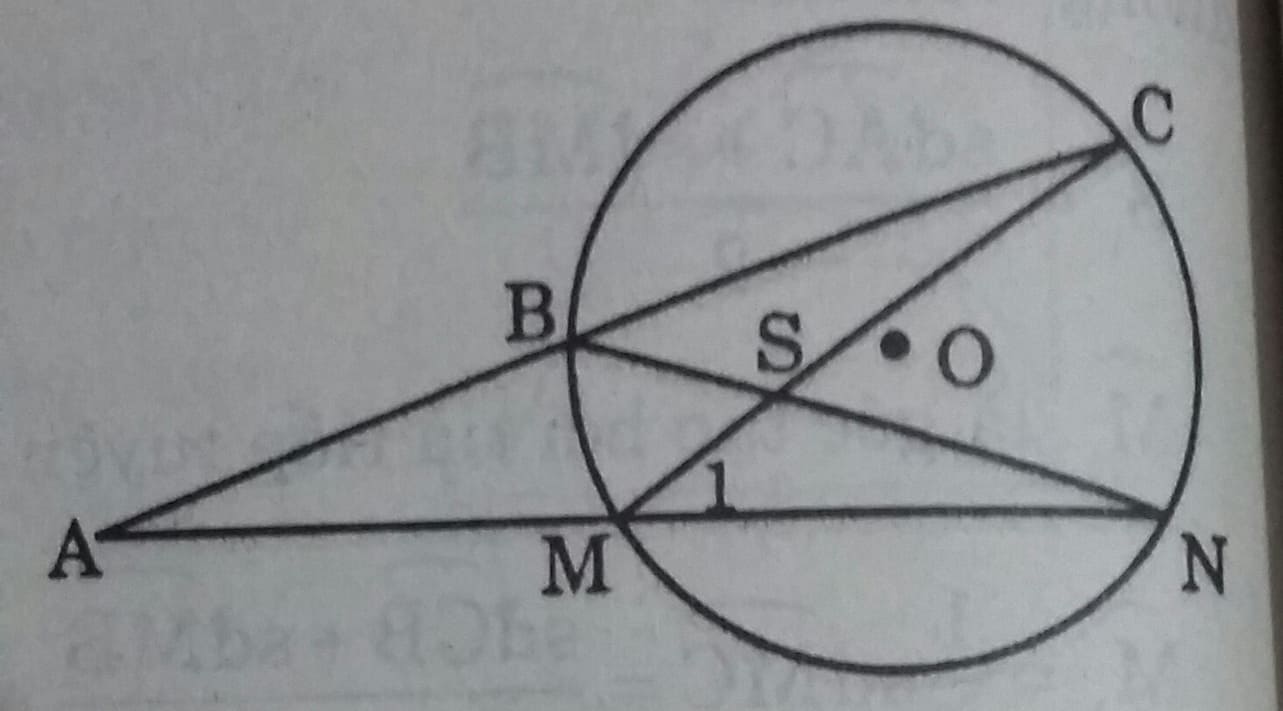
    Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn.

Hướng dẫn giải

    Góc \(\widehat{A}\) là góc có đỉnh ở bên ngoài đường tròn nên:

    \(\widehat{A}= ​​​​\dfrac{sđ \stackrel\frown{CN}-sđ \stackrel\frown{BM}}{2} \)

    Góc \(\widehat{BMS}\) là góc có đỉnh ở bên trong đường tròn nên:

    \(\widehat{BMS}= ​​​​\dfrac{sđ \stackrel\frown{CN}+sđ \stackrel\frown{BM}}{2} \\ Do \ đó \ \widehat{A}+ \widehat{BMS} = sđ \stackrel\frown{CN}\\ Mặt khác \widehat{CMN} = \dfrac{1}{2}sđ \stackrel\frown{CN}( \ góc \ nội \ tiếp \ chắn \ cung \ \stackrel\frown{CN})\\ Suy \ ra \ \widehat{A}+ \widehat{BSM}= 2. \widehat{CMN}\)