Bài tập 14 trang 64 SBT Toán 9 Tập 1
Bài tập 14 trang 64 SBT Toán 9 Tập 1
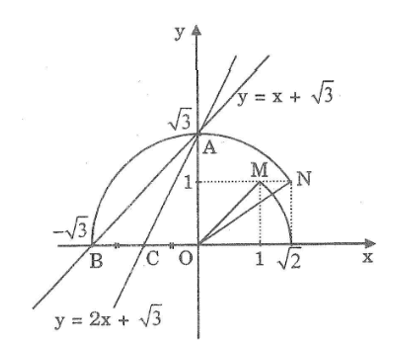
a. Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
y = x + \(\sqrt 3 \) (1)
y = 2x + \(\sqrt 3 \) (2)
b. Gọi giao điểm của đường thẳng y = x + \(\sqrt 3 \) với các trục Ox, Oy theo thứ tự là A, B và giao điểm của đường thẳng y = 2x + \(\sqrt 3 \) với các trục Ox, Oy theo thứ tự là A, C. Tính các góc của tam giác ABC.
a. *Vẽ đồ thị của hàm số y = x + \(\sqrt 3 \)
Cho x = 0 thì y = \(\sqrt 3 \) . Ta có: A(0; √3 )
Cho y = 0 thì x + \(\sqrt 3 \) = 0 => x = - √3 . Ta có: B(-\(\sqrt 3 \) ; 0)
Cách tìm điểm có tung độ bằng √3 trên trục Oy:
- Dựng điểm M(1; 1). Ta có: OM = √2
- Dựng cung tròn tâm O bán kính OM cắt trục OX tại điểm có hoành độ bằng 2
- Dựng điểm N(1; \(\sqrt 2 \) ). Ta có: ON = √3
- Vẽ cung tròn tâm O bán kính ON cắt trục Oy tại A có tung độ 3 cắt tia đối của Ox tại B có hoành độ -3
Đồ thị của hàm số y = x + \(\sqrt 3 \) là đường thẳng AB.
*Vẽ đồ thị của hàm số y = 2x + \(\sqrt 3 \)
Cho x = 0 thì y = \(\sqrt 3 \) . Ta có: A(0; \(\sqrt 3 \) )
Cho y = 0 thì 2x + \(\sqrt 3 \) = 0 => x = - √3/2 . Ta có: C(-√3/2 ; 0)
Đồ thị của hàm số y = 2x + √3 là đường thẳng AC.
-- Mod Toán 9
Copyright © 2021 HOCTAP247