Bài tập 36 trang 70 SBT Toán 9 Tập 1
Bài tập 36 trang 70 SBT Toán 9 Tập 1
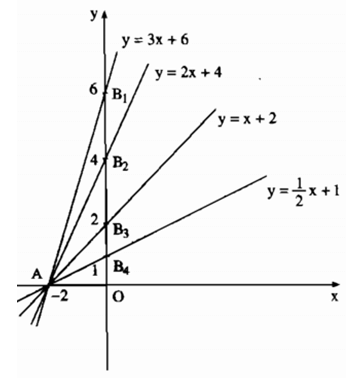
a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
y = 3x + 6; (1) y = 2x + 4 (2)
y = x + 2; (3) y = 1/2x + 1. (4)
b) Gọi giao điểm của các đường thẳng (1), (2), (3), (4) với trục là A và với trục tung lần lượt là B1, B2, B3, B4 ta có (B1 Ax) = α1; ∠(B2 Ax) = α2; ∠(B3 Ax) = α3; ∠(B4 Ax) = α4. Tính các góc α1, α2, α3, α4.
(Hướng dẫn: Dùng máy tính bỏ túi CASIO fx – 220 hoặc CASIO fx – 500A hoặc CASIO fx – 500MS… Tính tgα1, tgα2, tgα3, tgα4 rồi tính ra các góc tương ứng).
c) Có nhận xét gì về độ dốc của các đường thẳng (1), (2), (3) và (4) ?
a) - Đồ thị của hàm số y = 3x + 6 là đường thẳng đi qua hai điểm A(-2;0) và B1(0;6).
- Đồ thị của hàm số y = 2x + 4 là đường thẳng đi qua hai điểm A(-2;0) và B2(0;4).
- Đồ thị của hàm số y = x + 2 là đường thẳng đi qua hai điểm A(-2;0) và B3(0;2).
- Đồ thị của hàm số y = 1/2x + 1 là đường thẳng đi qua hai điểm A(-2;0) và B4(0;1).
b) Gọi ∠(B1Ax) = α1, ∠(B2Ax) = α2, ∠(B3 Ax) = α3, ∠(B4 Ax) = α4. Dùng máy tính bỏ túi CASIO fx – 220 tính tgα1, tgα2, tgα3, tgα4 và suy ra các góc tương ứng.
Ta có:
tgα1 = 3 ⇒ α1 ≈ 71o33’54,18’’.
tgα2 = 2 ⇒ α2 ≈ 63o26’5,82’’.
tgα3 = 1 ⇒ α3 ≈ 45o.
tgα4 = 1/2 ⇒ α4 ≈ 26o33’54,18’’.
c) Từ sự tăng dần của các hệ số góc: 1/2 < 1 < 2 < 3 và sự tăng dần của các góc α:
26o33’ < 45o < 63o26’ < 71o33’,
Rút ra nhận xét:
Với a > 0, khi a càng lớn thì góc tạo bởi đường thẳng y = ax + b và tia Ox càng lớn, và do đó độ dốc của đường thẳng (so với trục nằm ngang Ox càng lớn).
-- Mod Toán 9
Copyright © 2021 HOCTAP247