Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Đường trung trực của đoạn thẳng OA cắt Ox ở D, đường trung trực của đoạn thẳng OB cắt Oy ở E. Gọi C là giao điểm của hai đường trung trực đó. Chứng minh rằng:

a) CE = OD; b) CE ⊥ CD;

c) CA = CB; d) CA // DE;

e) Ba điểm A, B, C thẳng hàng.

Hướng dẫn giải

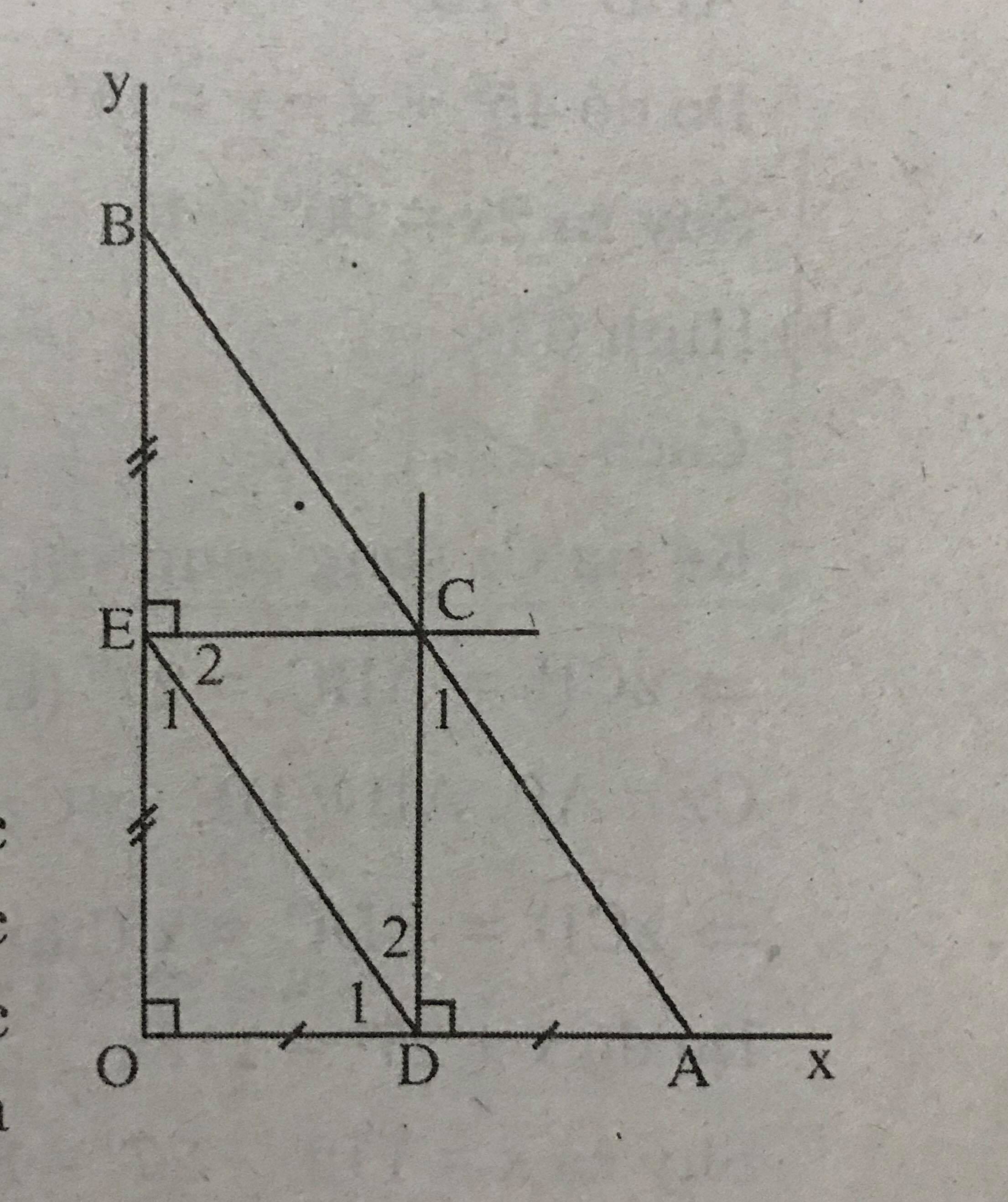
a) EC \(\perp\) Oy , OD \(\perp\) Oy (giả thiết)

=> EC // OD (1)

Tương tự : DC // OE (2)

Từ (1) và (2) kết hợp với \(\widehat{CEO}=90^0\)

=> OECD là hình chữ nhật

=> CE = OD

b) OECD là hình chữ nhật (câu a)

=> CE \(\perp\) CD

c) C là giao điểm của hai đường trung trực của hai cạnh OB và OA trong tam giác OAB => C nằm trên đường trung trực của cạnh AB (tính chất đồng quy của ba đường trung trực) => CA = CB

d) Tam giác CDA và tam giác DCE có :

EC = AD (= OD)

\(\widehat{C}=\widehat{D}=90^0\) (CE \(\perp\) CD , CD \(\perp\) Ox)

DC là cạnh chung

Nên tam giác CDA = tam giác DCE (c.g.c)

Suy ra \(\widehat{C_1}=\widehat{D_2} \Rightarrow CA // DE\) (có hai góc so le trong bằng nhau).

e) Chứng minh tương tự câu d ta có : CB // DE

Ta có : CA // DE và CB // DE nên CA và CB cùng nằm trên trên một đường thẳng.

Vậy ba điểm A, B, C thẳng hàng.