Trang chủ
Lớp 7
Toán Lớp 7 SGK Cũ
Ôn tập cuối năm - Hình học
Giải bài 69 trang 88 - Sách giáo khoa Toán 7 tập 2
Giải bài 69 trang 88 - Sách giáo khoa Toán 7 tập 2
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.
Hướng dẫn giải
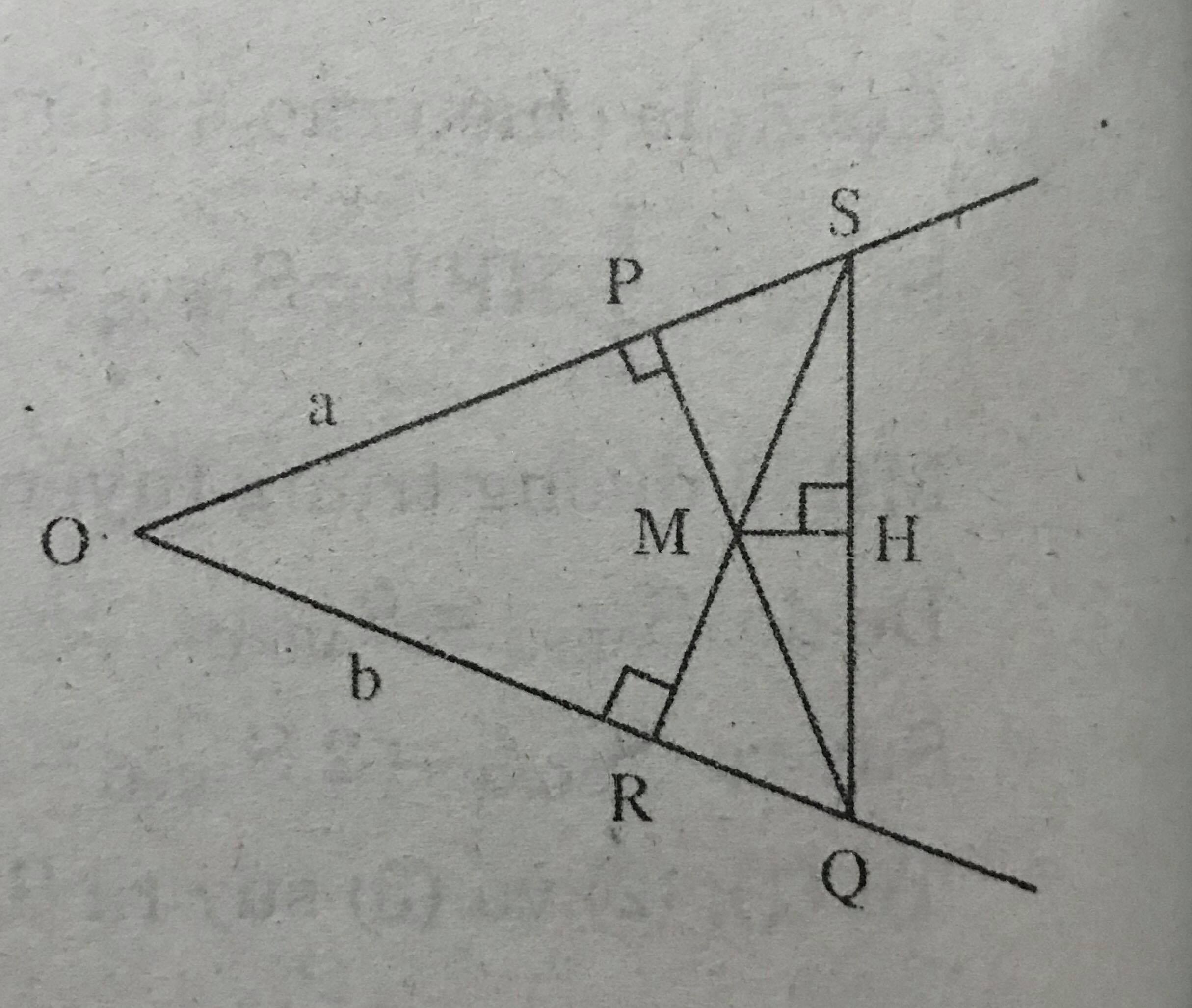
Gọi O là giao điểm của a và b, H là chân đường vuông góc kẻ từ M đến SQ.
QP vuông góc với OS suy ra QP là đường cao của tam giác SOQ.
SR vuông góc với OQ suy ra SR là đường cao của tam giác SOQ.
Do đó M là trực tâm của tam giác SOQ. Suy ra OM là đường cao của tam giác SOQ
Suy ra OM đi qua H ( Tính chất đường cao )
Vậy đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.
Copyright © 2021 HOCTAP247
