Giải bài 70 trang 88 - Sách giáo khoa Toán 7 tập 2

Đề bài

Cho A, B là hai điểm phân biệt và d là đường trung trực của đoạn thẳng AB.

a) Ta kí hiệu \(P_A\) là nửa mặt phẳng bờ d có chưa điểm A (không kể đường thẳng d). Gọi là một điểm của \(P_A\) và M là giao điểm của đường thẳng NB và d. Hãy so sánh NB với NM + MA; từ đó suy ra NA < NB.

b) Ta kí hiệu \(P_B\) là nửa mặt phẳng bờ d có chứa điểm B (không kể d). Gọi N’ là một điểm của \(P_B\). Chứng minh N’B < N’A.

c) Gọi L là một điểm sao cho LA < LB. Hỏi điểm L nằm ở đâu, trong \(P_A\), \(P_B\) hay trên d?

Hướng dẫn giải

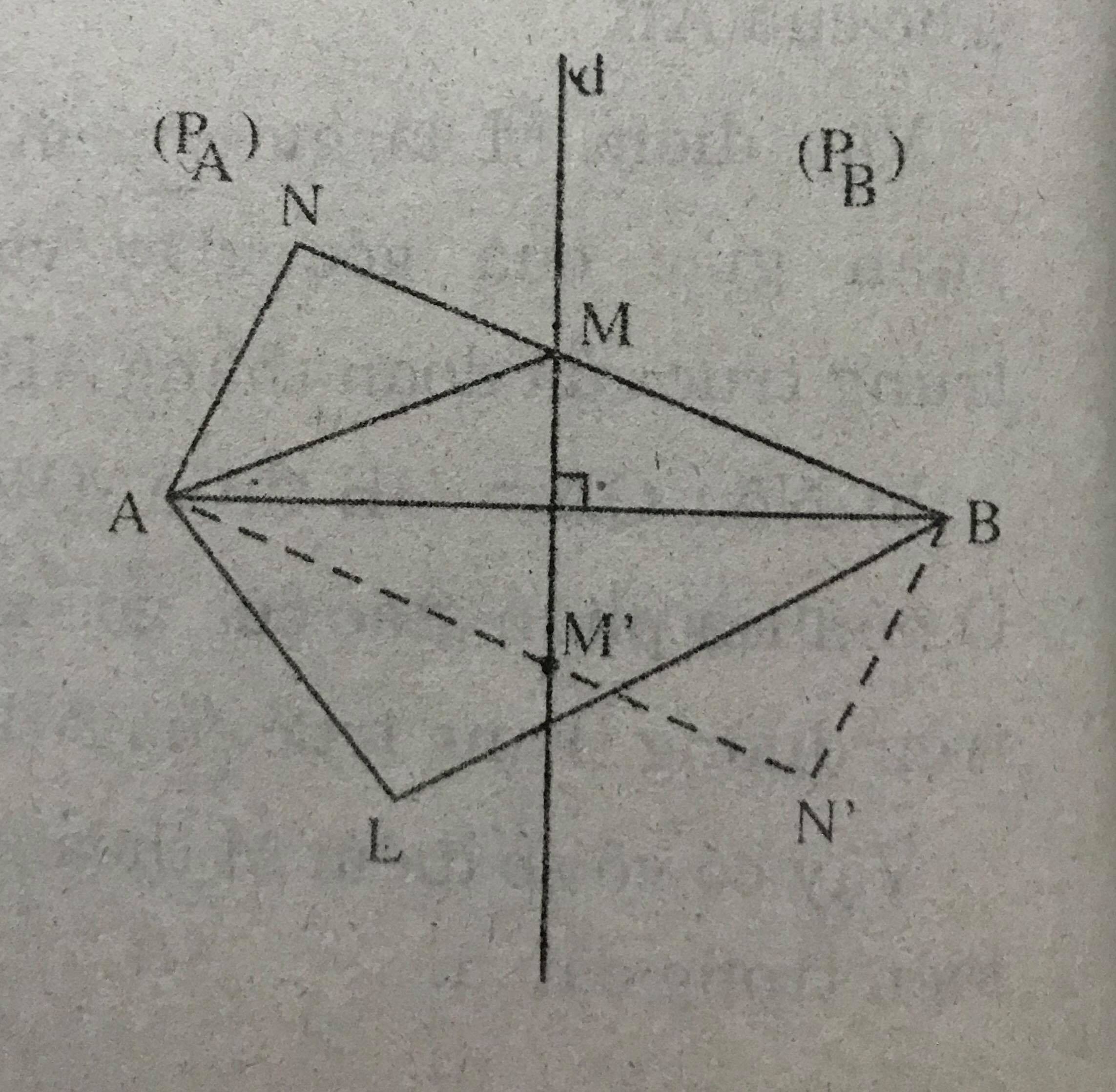
a) M thuộc đường trung trực của AB nên MA = MB.

Do đó : NM +  MA = NM + MB = NB (1)

Áp dụng bất đẳng thức tam giác và tam giác NMA có : NA < NM + MA

Suy ra NA < NB ( do (1)).

b) Gọi M' là giao điểm của N'A và d 

M' thuộc đường trung trực của AB nên M'A = M'B.

Do đó N'M' + M'A = N'M + M'B = N'A (2)

Áp dụng bất đẳng thức tam giác vào tam giác N'M'B có :

N'B < N'M' + MB .

Suy ra N'B < N'A (do (2))/

c) Nếu L thuộc d thì LA = LB ( d là đường trung trực của AB).

Điều này trái với giả thiết ( LA < LB ) nên L không thuộc d.

Nếu L thuộc \(P_b\) thì LB < LA ( theo câu b).

Điều này trái với giả thiết ( LA < LB) nên L không thuộc \(P_b\).

Vậy để LA < LB thì L phải thuộc \(P_a\)