Giải bài 9 trang 92 - Sách giáo khoa Toán 7 tập 2

Đề bài

Chứng minh rằng: Nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại A.

Ứng dụng: Một tờ giấy bị rách ở mép (h.65). Hãy dùng thước và compa dựng đường vuông góc ở cạnh AB tại A.

Hướng dẫn giải

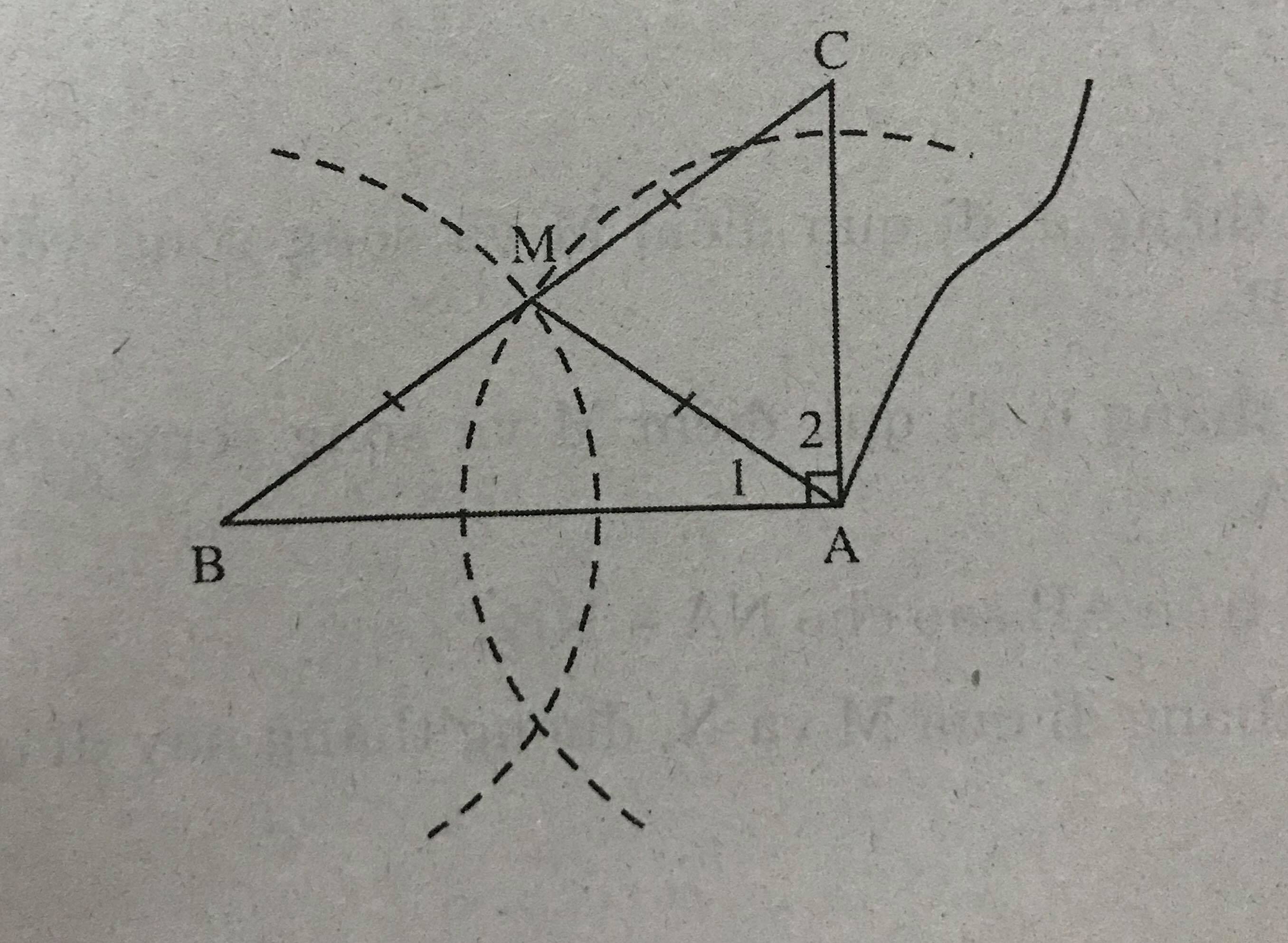
Kẻ đường trung tuyến AM của tam giác ABC => AM = \(\dfrac{1}{2}\)BC (gt)

MB = MC = \(\dfrac{1}{2}\)BC (tính chất đường trung tuyến)

=> MA = MB = MC

=> tam giác MAB , tam giác MAC cân tại M

=> \(\widehat{B}=\widehat{A_1},\widehat{C}=\widehat{A_1}\) (hai góc đáy của tam giác cân)

Do đó : \(\widehat{B}+\widehat{C}=\widehat{A_1}+\widehat{A_2}=\widehat{BAC}\)

Lại có : \(\widehat{B}+\widehat{C}+\widehat{BAC}=180^0\)

Nên \(\widehat{BAC}=\dfrac{180^0}{2}=90^0\)

Vậy tam giac ABC vuông tại A.

Ứng dụng : Dựng đường vuông góc với một đường thẳng cho trước :

Vẽ các cung tâm A và tâm B có cùng bán kính sao cho chúng cắt nhau tại C.

Trên tia đối của tia CB lấy điểm D sao cho CD = CB

Nối D với A, ta có DA vuông góc với AB.