Giải bài 7 trang 92 - Sách giáo khoa Toán 7 tập 2

Đề bài

Từ một điểm M trên tia phân giác của góc nhọn xOy, kẻ đường vuông góc với cạnh Ox (tại A), đường thẳng này cắt cạnh Oy tại B.

a) Hãy so sánh hai đoạn thẳng OAvà MA.

b) Hãy so sánh hai đoạn thẳng OB và OM.

Hướng dẫn giải

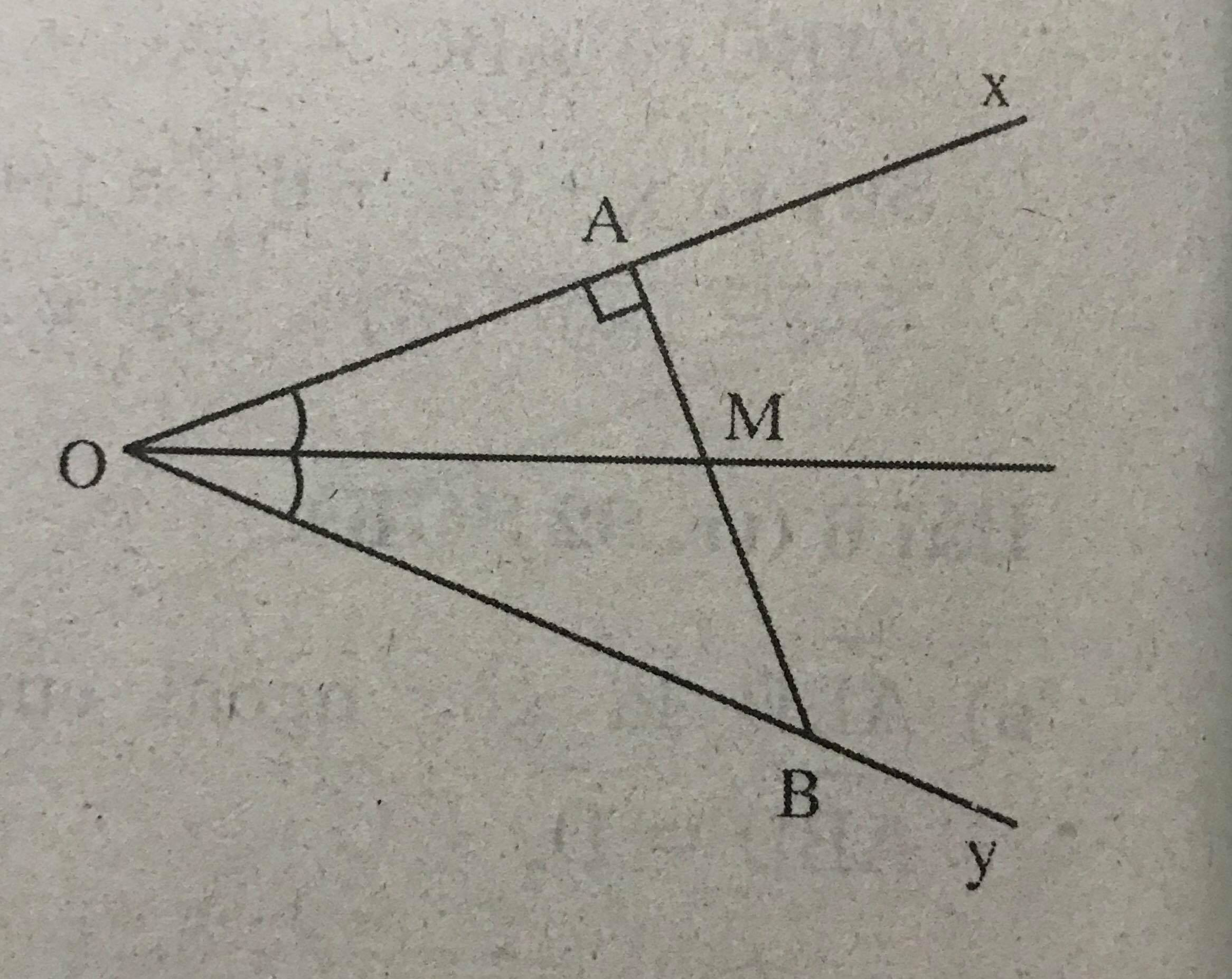
a) OM là tia phân giác của góc xOy

=> \(\widehat{AOM}=\dfrac{1}{2}\widehat{AOB}\)

Mà \(\widehat{AOB}<90^0\) (\(\widehat{AOB}\) là góc nhọn)

Nên \(\widehat{AOM}<45^0\)

Suy ra \(\widehat{OMA}>45^0\) (tổng hai góc nhọn trong tam giác vuông bằng 90 độ)

Vậy tam giác AOM có \(\widehat{OMA}>\widehat{AOM}\) nên OA > MA (cạnh đối diện với góc lớn hơn thì lớn hơn)

b) Tam giác OAM có góc A = 90 độ

Nên \(\widehat{OMA}<90^0\) (tổng ba góc trong tam giác bằng 180 độ)

=> \(\widehat{OMB}>90^0\) (góc kề bù của \(\widehat{OMA}\))

Tam giác có \(\widehat{OMB}>90^0\) nên OB > OM ( cạnh đối diện với góc tù là cạnh lớn nhất trong tam giác)