Giải bài 64 trang 87 - Sách giáo khoa Toán 7 tập 2

Đề bài

Gọi MH là đường cao của tam giác MNP. Chứng minh rằng: Nếu MN < MP thì HN < HP và \(\widehat{NMH}<\widehat{PMH}\) (yêu cầu xét hai trường hợp: khi góc N nhọn và khi góc N tù).

Hướng dẫn giải

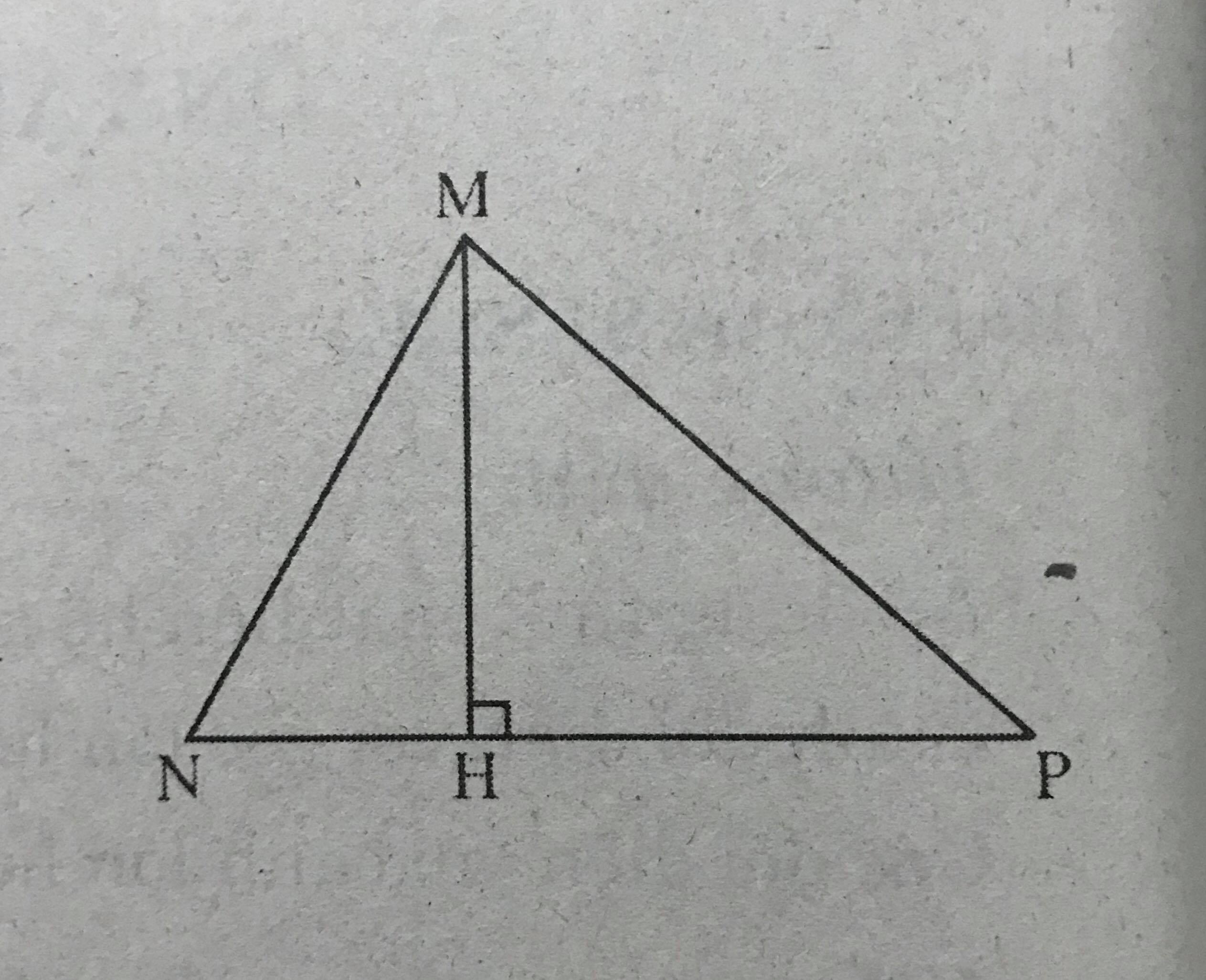
Khi góc N nhọn :

MH là đường cao của \(\Delta MNP\)

Suy ra MH vuông góc với NP

Do đường xiên MN < MP nên hình chiếu HN < HP

\(\widehat{NMH}=90^0 -\widehat{MNH}\)

\( \widehat{PMH}=90^0 -\widehat{MPH}\)

Lại có MP > MN nên \(\widehat{MNH} > \widehat{MPH}\) ( góc đối diện với cạnh lớn hơn thì lớn  hơn).

Do đó \(\widehat{NMH}<\widehat{PMH}\).

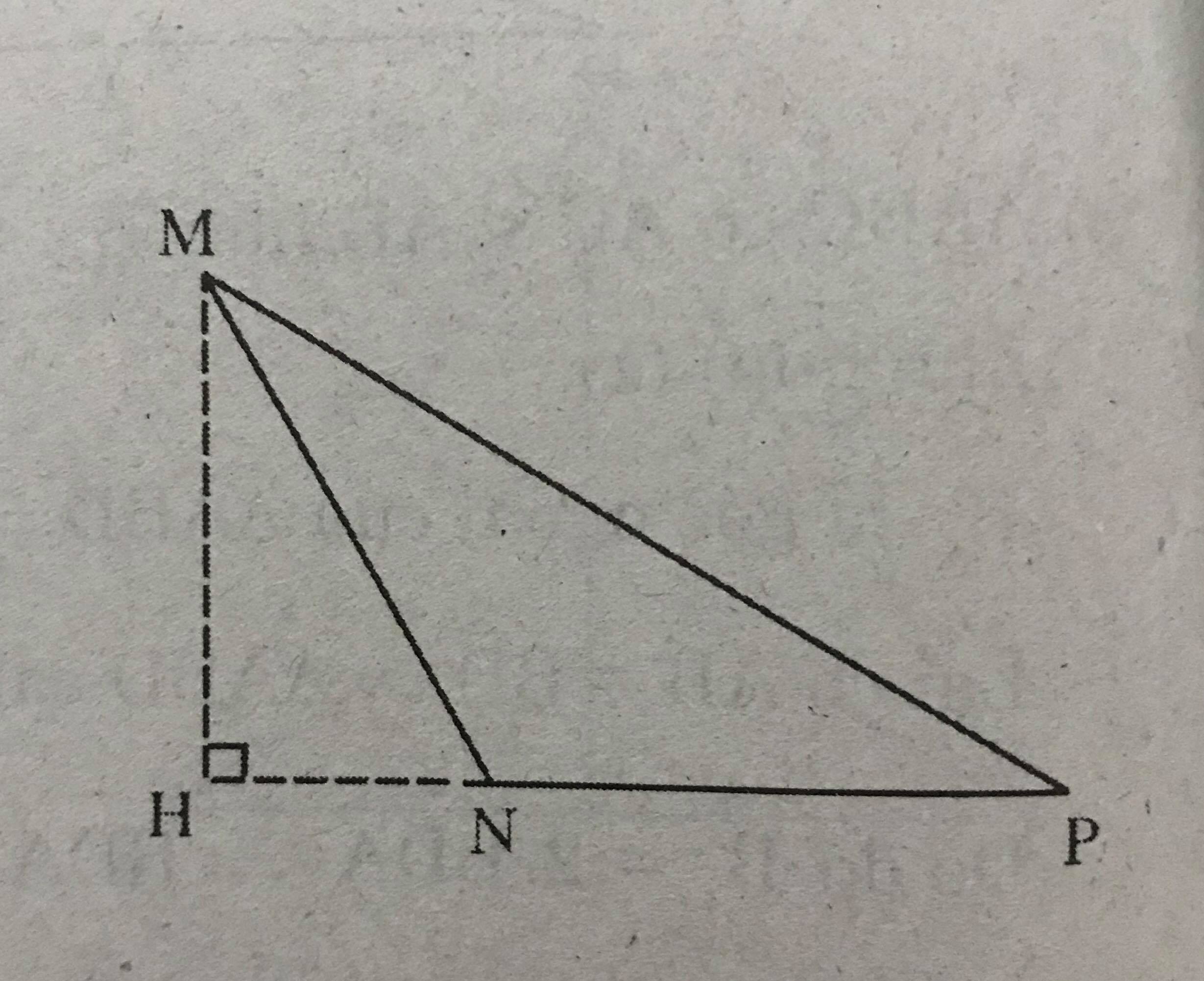
Khi góc N tù :

MH là đường cao của \(\Delta MNP\)

suy ra MH vuông góc với NP

Do đường xiên MN < MP nên hình chiếu HN < HP.

\(\widehat{NMH}=90^0 -\widehat{MNH}\)

\( \widehat{PMH}=90^0 -\widehat{MPH}\)

\(\widehat{MNH}\) là góc ngoài của \(\Delta MNP\) nên  \(\widehat{MNH} > \widehat{MPH}.\)

Do đó \(\widehat{NMH}<\widehat{PMH}\).