Giải bài 6 trang 92 - Sách giáo khoa Toán 7 tập 2

Đề bài

 Cho tam giác ADC (AD = DC) có góc ACD = 31 độ. Trên cạnh AC lấy một điểm B sao cho góc ABD = 88 độ. Từ C kẻ một tia song song với BD cắt tia AD ở E.

a) Hãy tính các góc DCE và DEC.

b) Trong tam giác CDE, cạnh nào lớn nhất? Tại sao?

Hướng dẫn giải

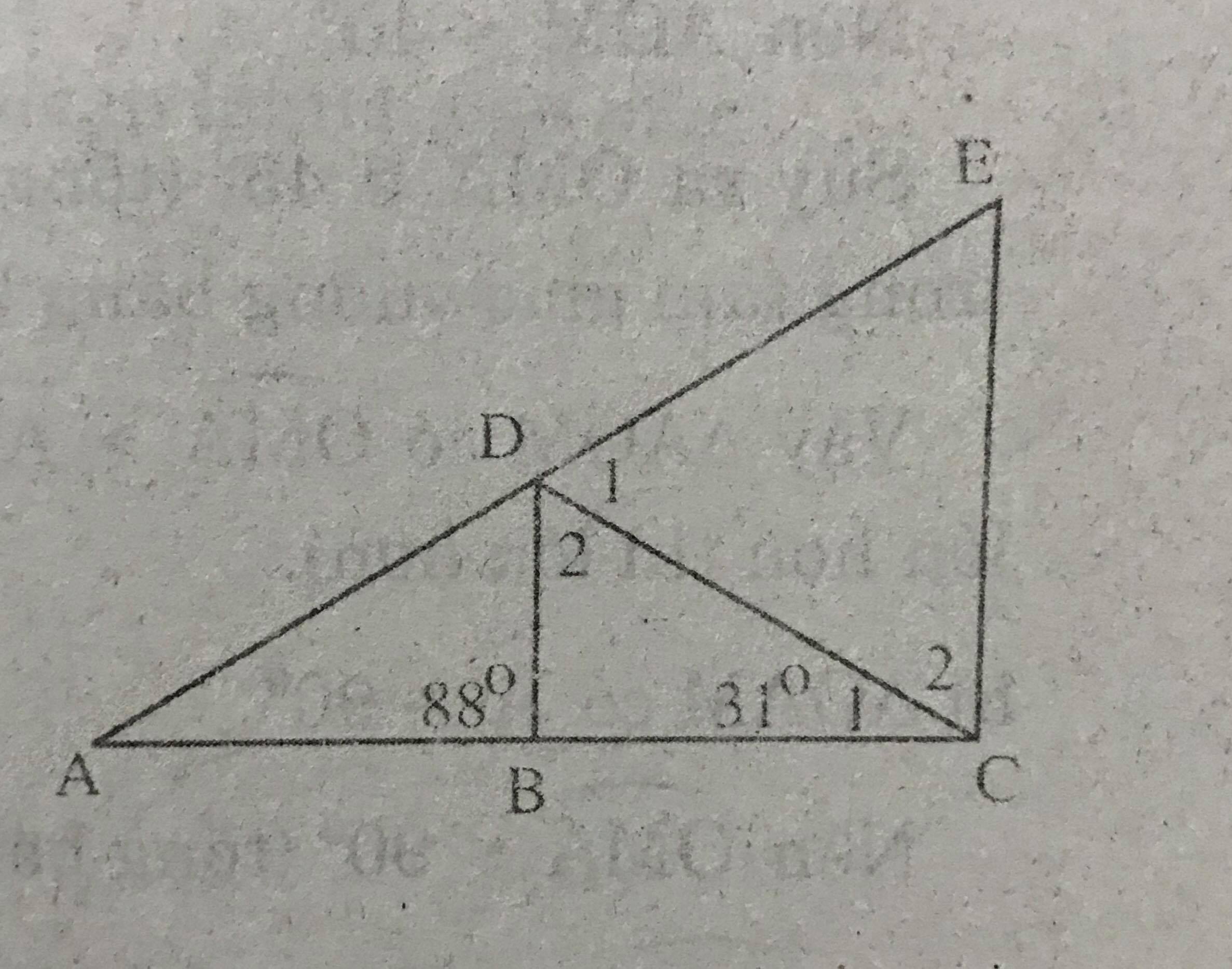
a) \(\widehat{ABD}\) là góc ngoài của tam giác DBC nên

\(\widehat{ABD}\) = \(\widehat{D_2}+\widehat{C_1}\)

=> \(\widehat{D_2}=\widehat{ABD}-\widehat{C_1}=88^0-31^0=57^0\)

BD // CE => \(\widehat{C_2}=\widehat{D_2}=57^0\) (hai góc so le trong)

Do đó \(\widehat{DCE}=57^0\)

Tam giác ADC cân tại D nên \(\widehat{A}=\widehat{C_1}=31^0\)

Tam giác AEC có : \(\widehat{A}+\widehat{C}+\widehat{E}=180^0\) (tính chất của tam giác)

=> \(\widehat{E}=180^0-\widehat{A}-\widehat{C}\)

=> \(\widehat{E}=180^0-31^0-88^0=61^0\)

b) Tam giác DEC có \(0\widehat{D_1}>\widehat{E}>\widehat{C_2} (62^0>61^0>57^0\) nên cạnh CE là cạnh lớn nhất (cạnh đối diện của góc lớn hơn thì lớn hơn).