Bài 28 trang 116 SGK Toán 9 tập 1

Đề bài

Cho góc \(xAy\) khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc \(xAy\) nằm trên đường nào?

Hướng dẫn giải

Sử dụng tính chất của hai tiếp tuyến cắt nhau: Cho \((O;R)\) với hai tiếp tuyến \(AB,\ AC\). Khi đó:  \(AO\) là phân giác của góc \(BAC\)

Lời giải chi tiết

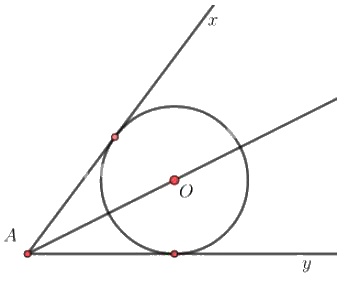
Gọi \(O\) là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc \(xAy\). Khi đó \(Ox,\ Oy\) là hai tiếp tuyến của đường tròn \((O)\). Theo tính chất của hai tiếp tuyến cắt nhau ta có:

\(\widehat {xAO} = \widehat {y{\rm{A}}O}\)

Hay \(AO\) là tia phân giác của góc \(xAy\). Vậy tập hợp tâm các đường tròn tiếp xúc với hai cạnh của góc \(xAy\) nằm trên tia phân giác của góc \(\widehat{xAy}\).