Đề kiểm tra 15 phút - Đề số 1 - Bài 6 - Chương 2 - Hình học 9

Đề bài

Cho đường tròn (O; R) và một điểm A sao cho \(OA = 2R.\) Vẽ các tiếp tuyến AB, AC (B, C là các tiếp điểm). Đường thẳng OA cắt BC tại H, cắt cung nhỏ và cung lớn BC lần lượt tại M và N.

a. Chứng minh rằng: \(OA ⊥ BC\) và \({R^2} = OA.HM\)

b. Vẽ cát tuyến bất kì ADE. Gọi K là trung điểm của DE. Chứng tỏ năm điểm A, B, O, K, C thuộc cùng một đường tròn.

Hướng dẫn giải

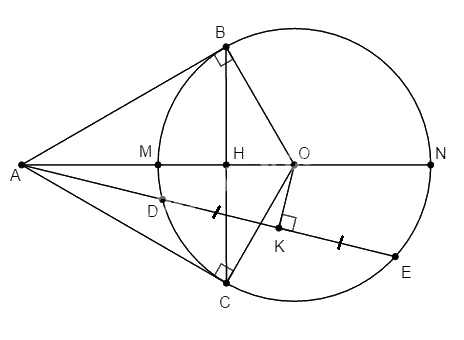
a. AB và AC là hai tiếp tuyến của đường tròn (O) ta có \(AB = AC\), lại có \(OB = OC (=R)\) nên OA là đường trung trực của đoạn BC \(⇒ OA ⊥ BC.\)

Ta có: \(OA = 2R (gt)\)

\(⇒ MA = OA - MO = 2R - R = R\)

Hay M là trung điểm của AO.

∆ABO có BM là trung tuyến nên:

\(BM = MO = {{AO} \over 2} = R\)

Vậy ∆BMO đều. Do đó đường cao BH cũng đồng thời là đường trung tuyến nên \(HM = HO = {R \over 2}\)

∆ABO vuông có BH là đường cao nên \(O{B^2} = OA.OH\) (hệ thức lượng)

hay \({R^2} = OA.HM\)

b. K là trung điểm của \(DE ⇒ OK ⊥ DE\) (định lí đường kính dây cung)

Do đó ∆AKO vuông tại K có OA là cạnh huyền, lại có các tam giác ABO, ACO vuông cũng có OA là cạnh huyền. Vì vậy năm điểm A, B, O, K, C thuộc cùng một đường tròn có đường kính OA.