Giải bài 27 trang 115 - Sách giáo khoa Toán 9 tập 1

Đề bài

    Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.

Hướng dẫn giải

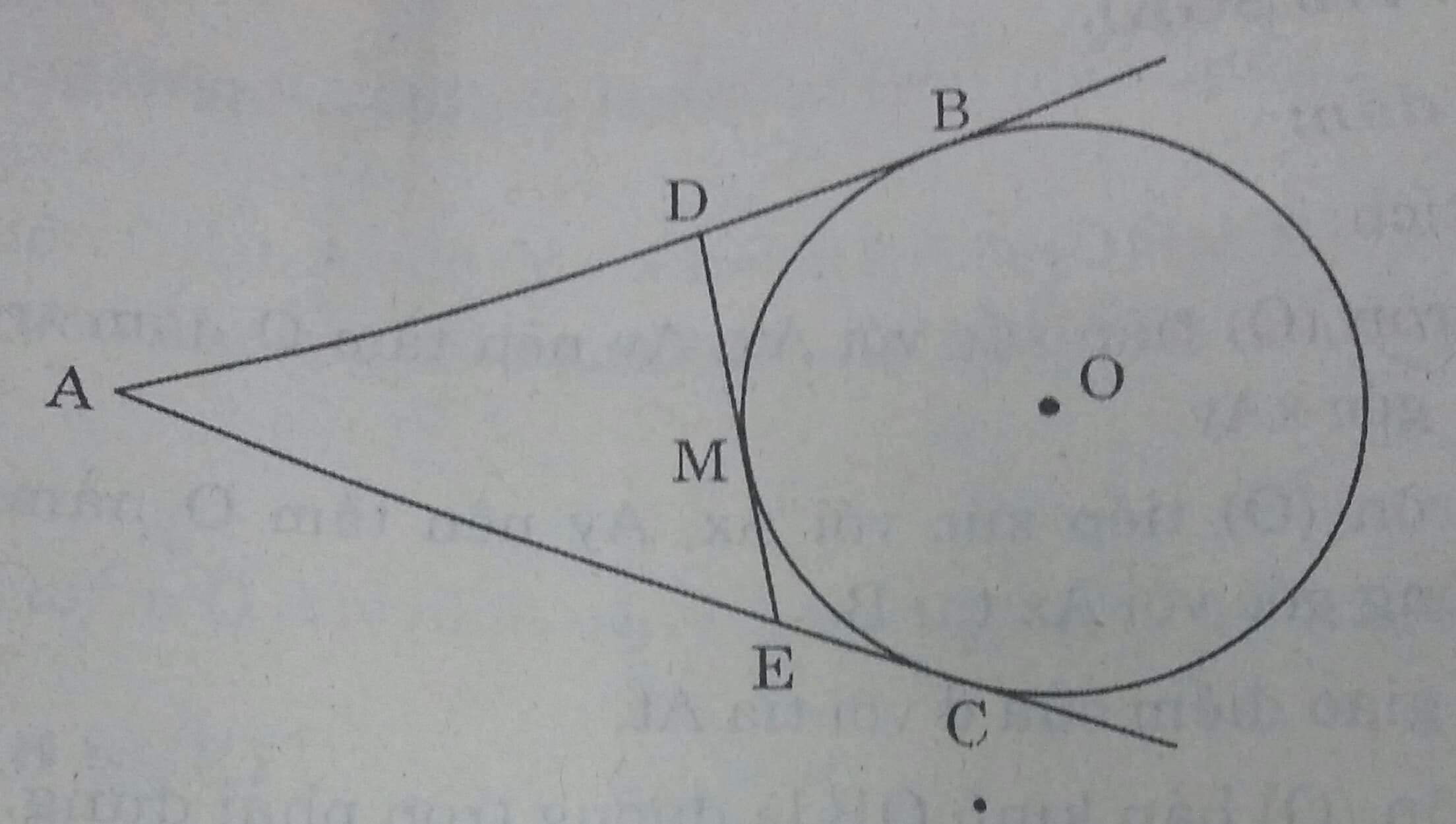
    Ta có: AB, AC là hai tiếp tuyến \( \Rightarrow AB=AC\).

  DB, DM là hai tiếp tuyến \( \Rightarrow DB= DM\)

  EC, EM là hai tiếp tuyến \( \Rightarrow EC= EM\)

 Chu vi tam giác \(\Delta ADE\) = AD+ DE+ EA= AD+ DM+ ME+ EA 

                                         = AD + DB + EC + EA 

                                          = AB+AC ( đpcm)