Đề kiểm tra 15 phút - Đề số 10 - Bài 6 - Chương 2 - Hình học 9

Đề bài

Một đường thẳng d cố định nằm ngoài đường tròn (O; R). Lấy M bất kì trên d. Từ M kẻ hai tiếp tuyến MP và MQ đến đường tròn (O) (P, Q là các tiếp điểm). Kẻ \(OH ⊥ d\). Dây cung PQ cắt OH ở I, cắt OM ở K. Chứng minh rằng :

a. \(OH.OI = OM.OK = {R^2}\)

b. Khi M thay đổi trên đường thẳng d thì  vị trí của điểm I luôn luôn cố định.

Hướng dẫn giải

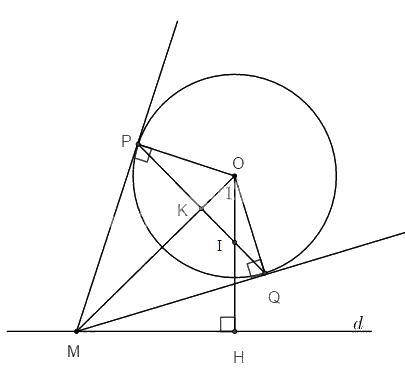
a. Ta có: MP và MQ là hai tiếp tuyến của (O) nên \(MP = MQ\), lại có \(OP = OQ (=R)\)

Do đó MO là đường trung trực của đoạn PQ nên \(MO ⊥ PQ\)

Lại có : ∆MQO vuông có QK là đường cao nên \(OM.OK = O{Q^2} = {R^2}\)

Mặt khác, hai tam giác vuông OKI và OHM đồng dạng (vì có \({\widehat O_1}\) chung)

\( \Rightarrow {{OK} \over {OH}} = {{OI} \over {OM}}\)

\(\Rightarrow OH.OI = OM.OK = {R^2}\,\left( 1 \right)\)

b. Từ (1) \( \Rightarrow OI = {{{R^2}} \over {OH}}\) (không đổi vì O cố định và d cố định), do đó I cố định.