Giải bài 32 trang 116 - Sách giáo khoa Toán 9 tập 1

Đề bài

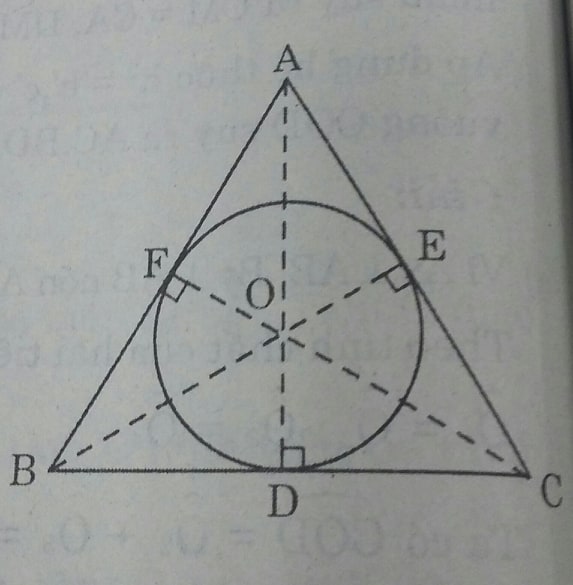
Cho tam giác đều ABC ngoại tiếp đường tròn bán kính 1cm. Diện tích của tam giác ABC bằng: 

Hướng dẫn giải

   Giải: 

   Tâm O của đường trọn nội tiếp tam giác là giao điểm của các đường phần giác. Vì tam giác ABC là tam giác đều nên tâm O cũng là giao điểm của các đường cao, trung tuyến. 

  Do đó: AD= 3OD= 3(cm) 

  Mặt khác: \(AD= \frac{BC\sqrt{3} }{2}\)

  Nền \(BC = \frac{2AD}{\sqrt{3}}= \frac{\sqrt{2.3} }{\sqrt{3}}=2 \sqrt{3}\)(cm) 

  \(S _ {\Delta ABC} = \frac{AD.BC}{2}= \frac{2 \sqrt{3}.3}{2}=3\sqrt{3}(cm^2)\) 

  Câu trả lời đúng là D.