Đề kiểm tra 15 phút - Đề số 7 - Bài 6 - Chương 2 - Hình học 9

Đề bài

Từ điểm M ở ngoài đường tròn (O; R), kẻ đường thẳng qua O cắt đường tròn ở hai điểm A và B.

a. Chứng minh rằng : \(MA.MB = M{O^2} - {R^2}\)

b. Kẻ cát tuyến thứ hai MCD với đường tròn. Chứng minh: \(MC.MD = MA.MB.\)

Hướng dẫn giải

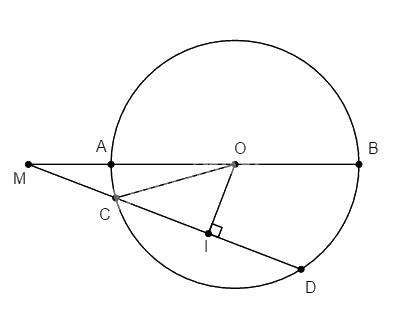
a. Có \(\eqalign{  MA.MB &= \left( {MO - OA} \right).\left( {MO + OB} \right)  \cr  &  = \left( {MO - R} \right).\left( {MO + R} \right)  \cr  &  = M{O^2} - {R^2}\,\left( 1 \right) \cr} \)

b. Kẻ \(OI ⊥ CD\), ta có:

\(IC = ID\) (định lí đường kính dây cung)

Ta có:

\(MC.MD = \left( {MI - IC} \right).\left( {MI + ID} \right) \)

\(\;= M{I^2} - I{C^2}\) (vì \(IC = ID\) theo chứng minh trên)

\(\eqalign{  &  = \left( {M{O^2} - O{I^2}} \right) - \left( {O{C^2} - O{I^2}} \right)  \cr  &  = M{O^2} - O{I^2} - O{C^2} + O{I^2} \cr&= M{O^2} - O{C^2}  \cr  &  = M{O^2} - {R^2}\,\left( 2 \right) \cr} \)

Từ (1) và (2) \( \Rightarrow MA.MB = MC.MD \)\(\;= M{O^2} - {R^2}\)