Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 2 - Hình học 9

Đề bài

Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc (O), tiếp tuyến A của (O) cắt BC tại D. Gọi M là trung điểm của AD.

a. Chứng minh MC là tiếp tuyến của (O).

b. Chứng minh \(MO ⊥ AC\) tại trung điểm I của AC.

Hướng dẫn giải

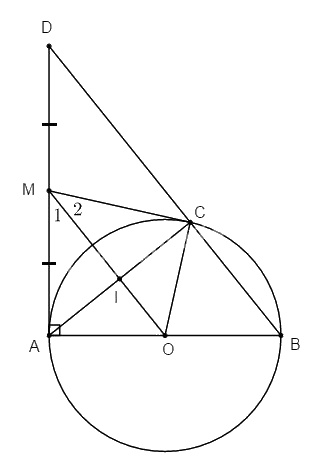
a. Ta có: \(\widehat {ACB} = 90^\circ \) (chắn nửa đường tròn)

\( \Rightarrow \widehat {ACD} = 90^\circ \) (kề bù)

∆ACD vuông có CM là đường trung tuyến

\( \Rightarrow CM = MA = {{AD} \over 2}\)

Do đó hai tam giác vuông MCO và MAO bằng nhau (c.c.c)

\( \Rightarrow \widehat {MCO} = \widehat {MAO} = 90^\circ \) hay MC là tiếp tuyến của (O)

b. Ta có: \(MA = MC\) (tính chất hai tiếp tuyến cắt nhau)

\(OA = OC (=R)\)

\(⇒ OM\) là đường trung trực của đoạn AC hay \(OM ⊥ AC.\)