Giải bài 29 trang 116 - Sách giáo khoa Toán 9 tập 1

Đề bài

   Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.

Hướng dẫn giải

   Giải: 

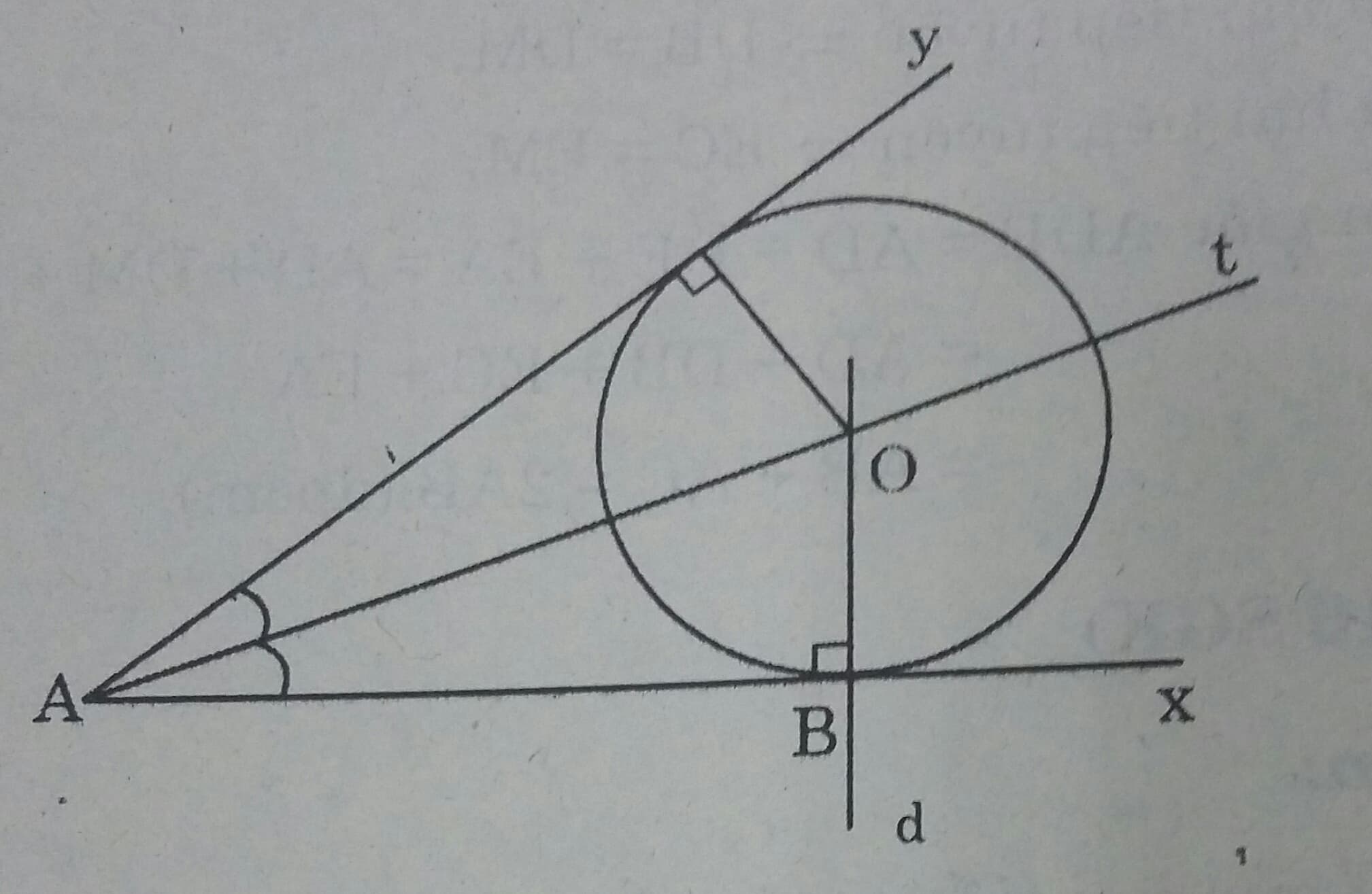
   Phân tích: 

  Giả sử đã dựng được đường tròn (O) thỏa mãn đề bài. Tâm O phải thỏa mãn hai điều kiện: 

  Đường tròn (O) tiếp xúc với Ax, Ay nên tâm O nằm trên tia phân giác At của góc xAy. 

   Đường tròn (O) tiếp xúc với Ax, By nên tâm O năm trên đường thẳng d vuông góc với Ax tại B. 

 Vậy O là giao điểm của d với tia At. 

   Đường tròn (O) bán kính OB là đường tròn phải dựng. 

 * Cách dựng: 

 Dựng tia phân giác At của  \(\widehat{xAy}\)

 Dựng đương thẳng  vuông góc với Ax tại B.

 At cắt d tai O.  

 Dựng đường tròn (O,OB) đó là đường tròn phải dựng. 

 * Chứng minh: 

 Vì \(O \in d\ nên\ OB \perp Ax\) do đó Ax tiếp xúc với (O) tại B. 

 Vì \(O \in At\) nên khoảng cách từ O đến Ay bằn Ob do đó Ay tiếp xúc với (O). 

   Biện luận: 

 d cắt At tại O duy nhất nên bài toán luôn có một nghiệm hình.