Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Bài 6. Cung chứa góc
Đề kiểm 15 phút - Đề số 5 - Bài 6 - Chương 3 - Hình học 9
Đề kiểm 15 phút - Đề số 5 - Bài 6 - Chương 3 - Hình học 9
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho ∆ABC đều nội tiếp trong đường tròn (O). Một điểm D di động trên cung nhỏ BC. Trên đoạn DA lấy DK = DB.
a) Chứng tỏ ∆BDK đều.
b) Khi D di chuyển trên cung BC thì K chuyển động trên đường nào ?
Hướng dẫn giải
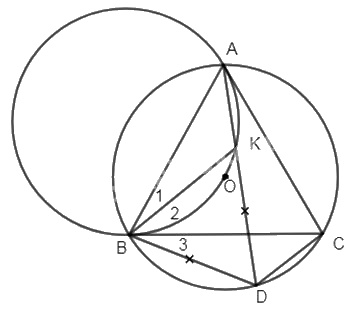
a) Ta có: \(DK = DB\) nên \(∆BDK\) cân có \(\widehat {BDK} = \widehat {BCA} = 60^\circ \) ( góc nôi tiếp cùng chắn cung AB) nên \(∆BDK\) đều.
b) \(∆BDK\) luôn là tam giác đều
\( \Rightarrow \widehat {BDK} = 60^\circ \) ( không đổi)
\( \Rightarrow \widehat {BKA} = 180^\circ - 60^\circ = 120^\circ \) ( không đổi)
Hai điểm A và B cố định.
Do đó K thuộc cung chứa góc 120º dựng trên đoạn AB ( cung AKB).
Copyright © 2021 HOCTAP247
