Giải bài 48 trang 87 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Cho hai điểm A, B cố định. Từ A vẽ các tiếp tuyến với các đường tròn tâm B có bán kính không lớn hơn AB. Tìm quỹ tích các tiếp điểm.

Hướng dẫn giải

    Trường hợp  đường tròn tâm B có bán kính nhỏ hơn AB.

    Phần thuận:

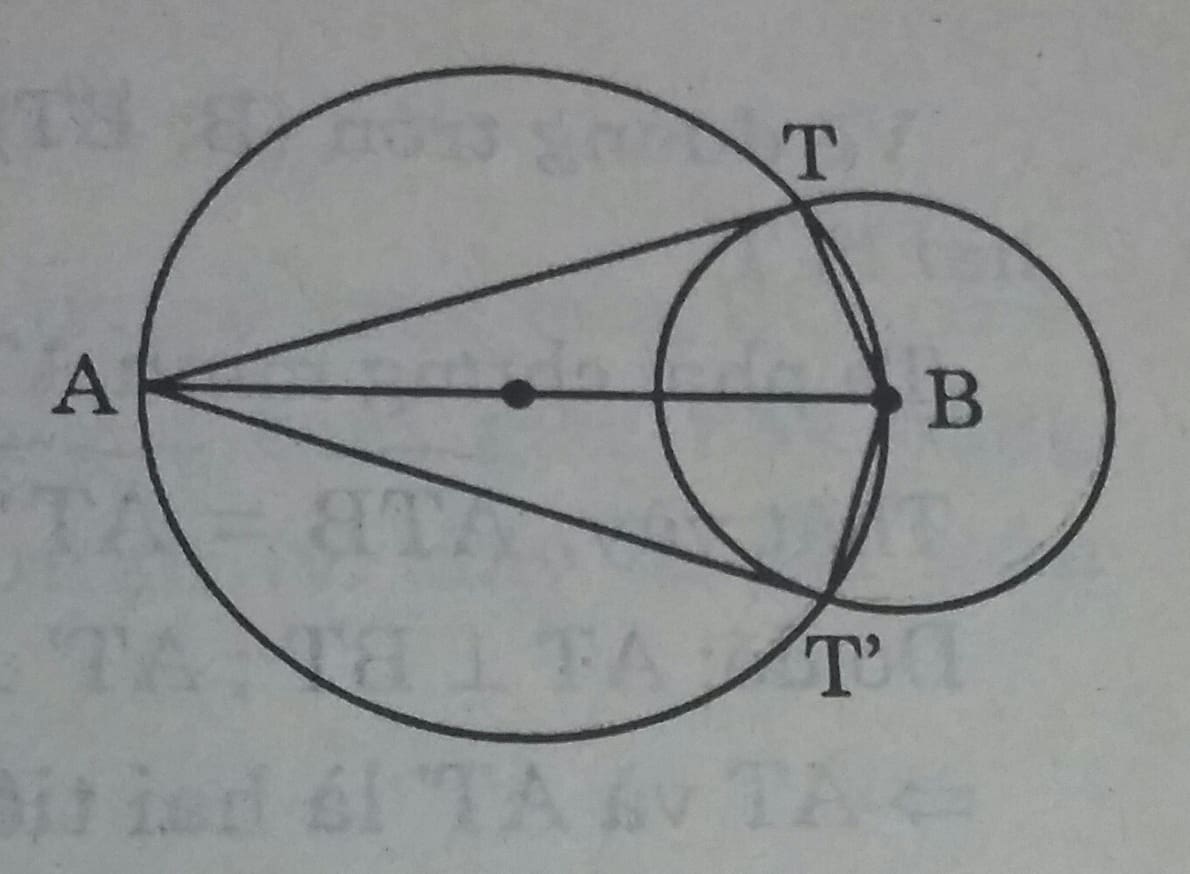
    AT và AT' là hai tiếp tuyến của đường tròn (B).

  \(\Rightarrow AT \perp BT; AT' \perp BT' \\\Rightarrow \widehat{ATB}=\widehat{AT'B}= 90^0\)

    Vậy T và T' trên đường tròn đường kính AB( trừ hai điểm A và B).

    Phần đảo:

   Lấy điểm T bất kì nằm trên đường tròn đường kính AB(T   khác A và B)

   Vẽ đường tròn( B; BT) cắt đường tròn đường kính AB tại điểm thứ hai là T'.

  Ta phải chứng minh AT và AT' là các tiếp tuyến của đường tròn (B).

    Thật vậy, \( \widehat{ATB}=\widehat{AT'B}=90^0\)( góc nội tiếp chắn nửa đương tròn) 

    Do đó: \(AT \perp BT ; AT' \perp BT;\)

   \( \Rightarrow AT \ và \ AT'\) là hai tiếp tuyến của đường tròn (B).

    Kết luận:

    Quỹ tích các điểm T và T' là đường tròn đường kính AB( trừ hai điểm A và B).

  Trường hợp đường tròn tâm B có bán kính AB thì quỹ tích là điểm A.

  Trường hợp đường tròn tâm B có bán kính là AB thì quỹ tích là điểm A.

   Kết hợp cả hai trường hợp ta được quỹ tích cần tìm là đường tròn đường kính AB trừ điểm B.