Giải bài 50 trang 87 - Sách giáo khoa Toán 9 tập 2

Đề bài

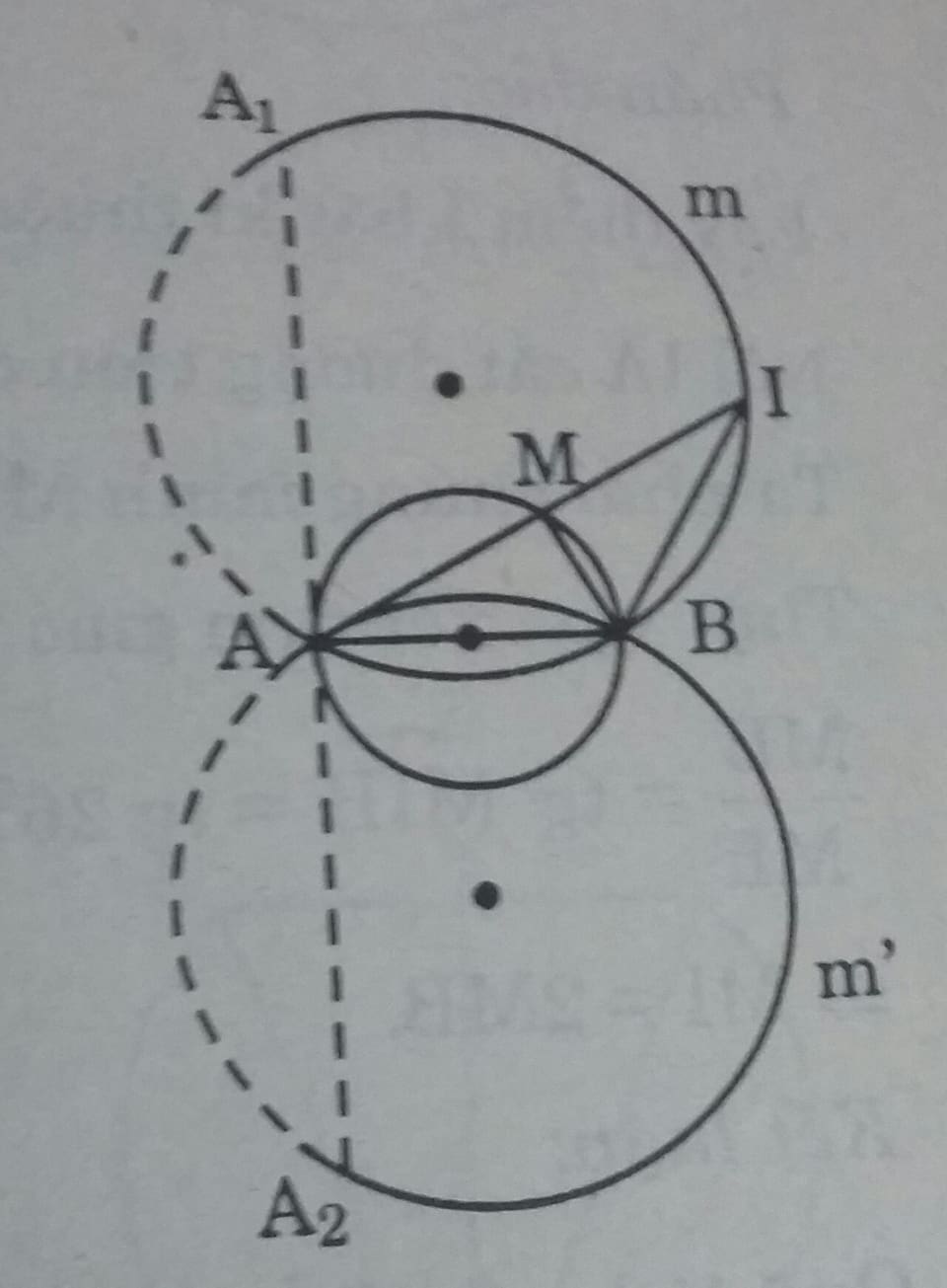
   Cho đường tròn đường kính AB cố định, M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 2MB.

Hướng dẫn giải

   a) Ta có \(\widehat{AMB}= 90^0 \) ( góc nội tiếp chắn nửa đường tròn)

  Xét \(\Delta MIB \) vuông tại M có: \(tg \widehat{MIB}= \dfrac{MB}{MI }=\dfrac{1}{2}\)

  \( \Rightarrow \widehat{MIB} \approx 26^34'\ \\ Vậy \widehat{AIB} \ không \ đổi.\)

  b) Phần thuận

  Điểm \(I\) nhìn đoạn AB cố định dưới một góc là \(26^034'\) nên điểm \(I\) nằm trên hai cung chứa góc  dựng trên đoạn thẳng AB.

  Khi điểm M trùng với A thì cát tuyễn AM trở thành tiếp tuyến \(A_1AA_2\). Khi đó điểm  \(I\)  trùng với \(A_1 \ hoặc \ A_2\)

  Vậy điểm \(I\) chỉ thuộc hai cung \( \stackrel\frown{A_1mB}\ và \stackrel\frown{A_2mB}\)

  Phần đảo: 

 Lấy điểm bất kì thuộc cung \( \stackrel\frown{A_1mB}\ và \stackrel\frown{A_2mB}\) 

  Nối \(IA\) cắt đường kính tại AB tại điểm M,

  Ta phải chứng minh \(MI = 2MB \)

  Thật vậy, xét tam giác vuông \(MBI\) ta có:

   \(\dfrac{MB}{MI}= tg \widehat{MIB}= tg \ 26^0 34 = \dfrac{1}{2} \Rightarrow MI = 2MB\)

  Quỹ tích các điểm \(I\) năm trên hao cung \( \stackrel\frown{A_1mB}\ và \stackrel\frown{A_2mB}\) chứa góc \(26^034'\) dựng trên đoạn thẳng AB ( \(A_1A_2 \perp AB \) taj A)