Tổng ôn Cung chứa góc - Toán học 9

Ở bài này sẽ gửi đến các bạn học bài giảng Cung chứa góc lớp 9 đầy đủ nhất, bao gồm như: thế nào là cung chứa góc, định lý cung chứa góc,... và làm bài tập cung chứa góc.Vậy những kiến thức vừa rồi bạn hãy cùng đi vào tìm hiểu trong bài viết dưới đây nhé!

A. Lý thuyết

I. Quỹ tích cung chứa góc

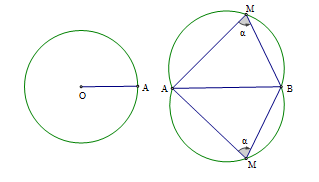
- Đoạn thẳng AB và góc \(\alpha\) (\(0^0 < \alpha < 180^0\)) cho trước thì quỹ tích các điểm M thỏa mãn góc AMB = \(\alpha\) là hai cung chứa góc \(\alpha\) dựng trên đoạn AB.

- Chú ý: 

• Hai cung chứa góc \(\alpha\) được nói ở phía trên đây là hai cung tròn đối xứng nhau qua đoạn thẳng AB. Trong đó hai điểm a và B được coi là thuộc quỹ tích.
• Đường tròn đường kính AB là quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông.

III. Phương pháp giải bài toán quỹ tích (tập hợp các điểm)

Nếu muốn đi chứng minh tập hợp (quỹ tích) cá điểm M thỏa mãn tính chất T là một hình H nào đó thì ta cần chứng minh hai phần sau:

- Phần thuận: Ta cần chứng minh mọi điểm có tính chất T đều thuộc hình H.

- Phần đảo: Ta cần chứng minh mọi điểm thuộc hình H đều có tính chất T.

=> Khi đã chứng minh được hai phần trên ta mới đi đến kết luận quỹ tích điểm M có tính chất T là hình H.

*Mẹo: Nên dự đoán hình H trước khi chứng minh bài toán tìm quỹ tích (tập hợp)...

B. Bài tập toán hình 9 Cung chứa góc

I. Các dạng toán Cung chứa góc thường gặp

1. Dạng 1: Quỹ tích là cung chứa góc \(\alpha\)

=> Phương pháp:

- Trong hình vẽ cần tìm đoạn cố định

- Xác định góc \(\alpha\) không đổi bằng cách nối điểm phải tìm với hai đầu đoạn thẳng cố định đó.

- Ta đi vào kết luận điểm phải tìm quỹ tích thuộc cung chứa góc \(\alpha\) dựng trên đoạn cố định.

2. Dạng 2: Chứng minh nhiều điểm thuộc đường tròn

=> Phương pháp:

Ta đi chứng minh có nhiều điểm cùng thuộc nửa mặt phẳng bờ AB và chúng đều cùng nhìn đoạn cố định AB dưới một góc không đổi.

3. Dạng 3: Dựng cung chứa góc

a) Bài toán mẫu: Cho trước đoạn thẳng AB và góc \(\alpha\) (\(0^0 < \alpha < 180^0\)) cho trước. Hãy tìm tập hợp các điểm M thỏa mãn góc AMB = \(\alpha\) 

b) Cách vẽ

- Bước 1: Trên đoạn thẳng AB vẽ đường trung trực d.

- Bước 2: Vẽ tia Ax tạo với đoạn thẳng AB một góc \(\alpha\)

- Bước 3: Vẽ đường thẳng Ay vuông góc với Ax, và gọi giao điểm của Ay và d là O.

- Bước 4: Vẽ cung AmB, tâm O, OA là bán kính để sao cho cung này nằm ở nửa mặt phẳng bờ AB không chứa tia Ax. Cung AmD được vẽ là cung chứa góc \(\alpha\)

II. Làm bài tập cung chứa góc

Câu 1: Đường tròn đường kính CD là quỹ tích của điểm nào dưới đây?

A. Quỹ tích của các điểm N nhìn đoạn thẳng CD cho trước dưới một góc 90 độ

B. Quỹ tích các điểm M thuộc đường trung trực của đường kính CD

C. Quỹ tích các điểm P nhìn đoạn thẳng CD cho trước dưới một góc 30 độ

D.  Quỹ tích các điểm Q nhìn đoạn thẳng CD cho trước dưới một góc 60 độ

=> Đáp án đúng: A.

=> Hướng dẫn: Áp dụng kiến thức quỹ tích cung chứa góc để giải bài tập.

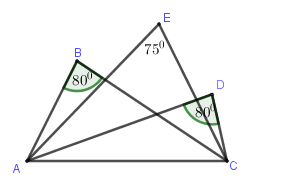
Câu 2: Đâu là kết luận đúng nhất cho hình vẽ dưới đây?

A, Điểm E thuộc cung chứa góc 80 độ dựng trên đoạn AC

B. B, E, D là ba điểm cùng thuộc cung chúa góc 80 độ dựng trên đoạn AC

C. A, B, C, D, E là năm điểm đều cùng thuộc một đường tròn

D. B, D là hai điểm thuộc cung chứa góc 80 độ dựng trên đoạn AC.

=> Đáp án đúng: D

=> Hướng dẫn: Ta quan sát hình vẽ sẽ thấy

• Hai điểm B, D đều thuộc cung chứa góc 80 độ và chắn đoạn AC
• Điểm E thuộc cung chứa góc 75 độ và chắn đoạn AC

Vậy đáp án D là đáp án đúng nhất

Câu 3: Cho trước đoạn thẳng AB và góc \(\alpha\) (\(0^0 < \alpha < 180^0\)) cho trước thì quỹ tích các điểm M thỏa mãn góc AMB =  \(\alpha\) là 

A, Một cung chứa góc \(\alpha\) dựng trên đoạn AB

B. Hai cung chứa góc \(\alpha\) dựng trên đoạn AB và không lấy đoạn AB.

C. Hai cung chứa góc \(\alpha\) dựng trên đoạn AB và hai cung này đối xứng nhau qua AB.

D. Hai cung chứa góc \(\alpha\) dựng trên đoạn AB và hai cung này không đối xứng nhau qua đoạn AB.

=> Đáp án đúng: C

=> Hướng dẫn: Xem lại lý thuyết mục I. Quỹ tích cung chứa góc

Câu 4: ABC là tam giác được cho trước, có BC cố định và góc A bằng 50 độ. Gọi giao điểm của ba đường phân giác trong của tam giác là D. Hãy tìm quỹ tích điểm D.

A. Một cung chứa góc 115 độ được dựng trên đoạn AB

B. Hai cung chứa góc 115 độ được dựng trên đoạn BC

C. Một cung chứa góc 115 độ được dựng trên đoạn BC

D.  Hai cung chứa góc 115 độ được dựng trên đoạn AB

=> Đáp án đúng: B

=> Hướng dẫn:

- Ta có: \(\widehat{A}=50^0 => \widehat{B}+ \widehat{C}=130^0\)

- Nên: \(\widehat{BDC} + \widehat{DBC} = \dfrac {130^0}{2}=65^0\) => \(\widehat{BDC} = 115^0\)

- Vậy đáp án đúng là B.

Câu 5: ABC là tam giác được cho trước, có BC cố định và góc A bằng 60 độ. Gọi giao điểm của ba đường phân giác trong của tam giác là D. Hãy tìm quỹ tích điểm D.

A. Một cung chứa góc 120 độ được dựng trên đoạn AB

B. Hai cung chứa góc 120 độ được dựng trên đoạn AC

C. Một cung chứa góc 120 độ được dựng trên đoạn BC

D.  Hai cung chứa góc 115 độ được dựng trên đoạn AB

=> Đáp án đúng: C

=> Hướng dẫn: Sử dụng tính chất tia phân giác tính góc BDC để từ đó suy ra được quỹ tích của cung chứa góc

Xem thêm >>> Bài tập SGK toán hình 9 cung chứa góc

Trên đây là toàn bộ lý thuyết cung chứa góc như định lý cung chứa góc, định nghĩa cung chứa góc mà muốn gửi đến cho các bạn học. Hy vọng các bài tập vận dụng bài 6 Cung chứa góc sẽ giúp bạn cung cổ thêm kiến thức lý thuyết, chúc các bạn học tập tốt <3