Giải bài 51 trang 87 - Sách giáo khoa Toán 9 tập 2

Đề bài

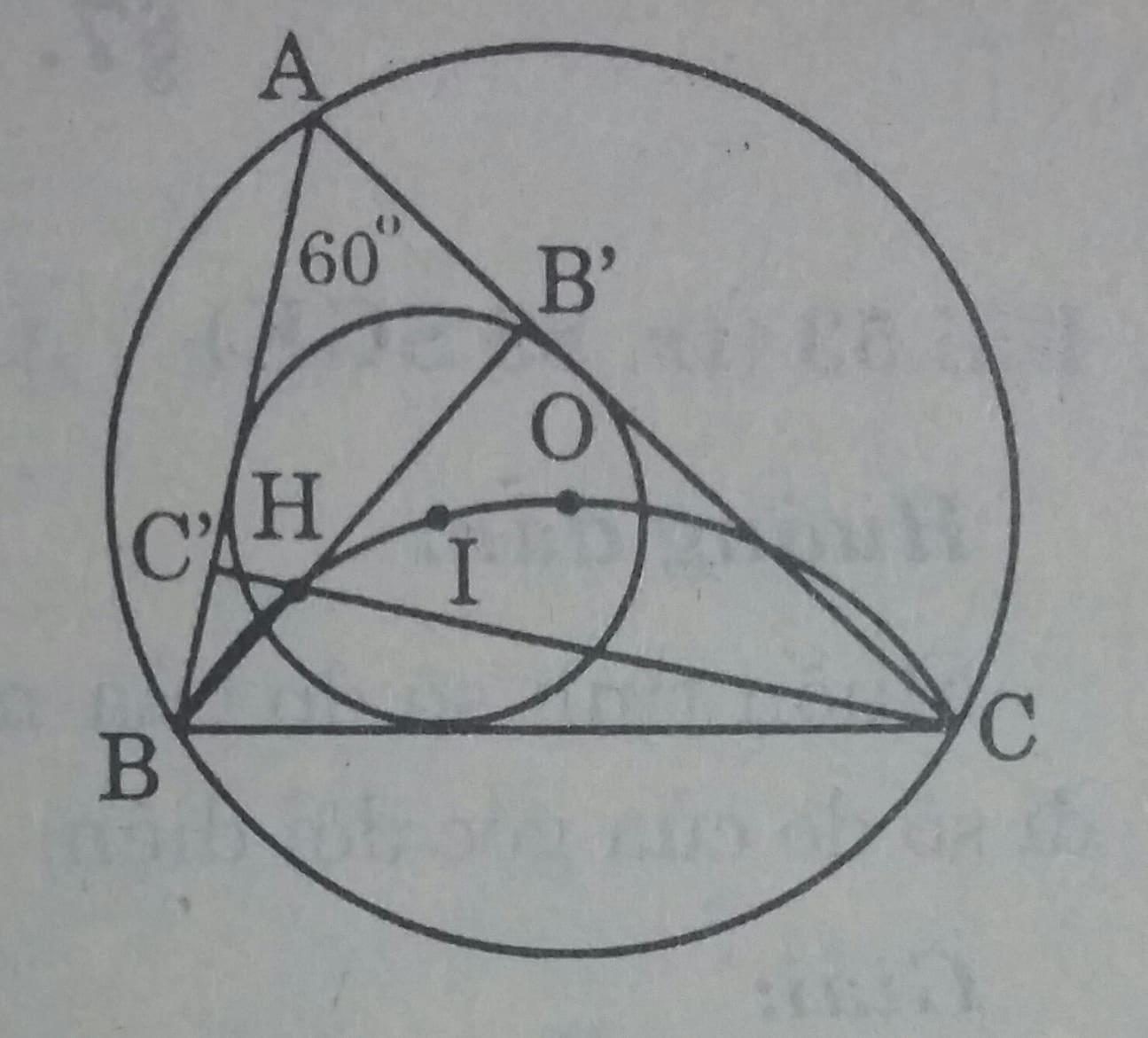
    Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với A = 60o. Gọi H là giao điểm của các đường cao BB'và CC'.

Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.

Hướng dẫn giải

   \(\Delta ABC \ có \ \widehat{A}= 60^0 \Rightarrow \widehat{B}+\widehat{C}= 120^0\)

  Xét \(\Delta BIC \) ta có:

  \( \widehat{BIC}= 180^0 - \dfrac{\widehat{B}+\widehat{C}}{2} = 180^0 - 60^0 = 120^0\ \widehat{BHC}= \widehat{B'HC'}= 180^0 - \widehat{A}= 120^0 \\ \Rightarrow \widehat{BOC}= 2 \widehat{A}= 2.60^0 = 120^0 ( góc \ nội \ tiếp \ và \ góc \ ở \ tâm \ cùng \ chắn \ một \ cung)\)

  Vậy \( \widehat{BIC}= \widehat{BHC}= \widehat{BOC}= 120^0 \)

   Suy ra các điểm \(I,H,O\) nằm trên cung chứa góc 120 dựng trên đoạn thẳng BC.

   Do đó 5 điểm \(I,H,O,B,C\) cùng thuộc một đường tròn.