Giải bài 44 trang 86 - Sách giáo khoa Toán 9 tập 2
Tóm tắt bài
Đề bài
Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.
Hướng dẫn giải
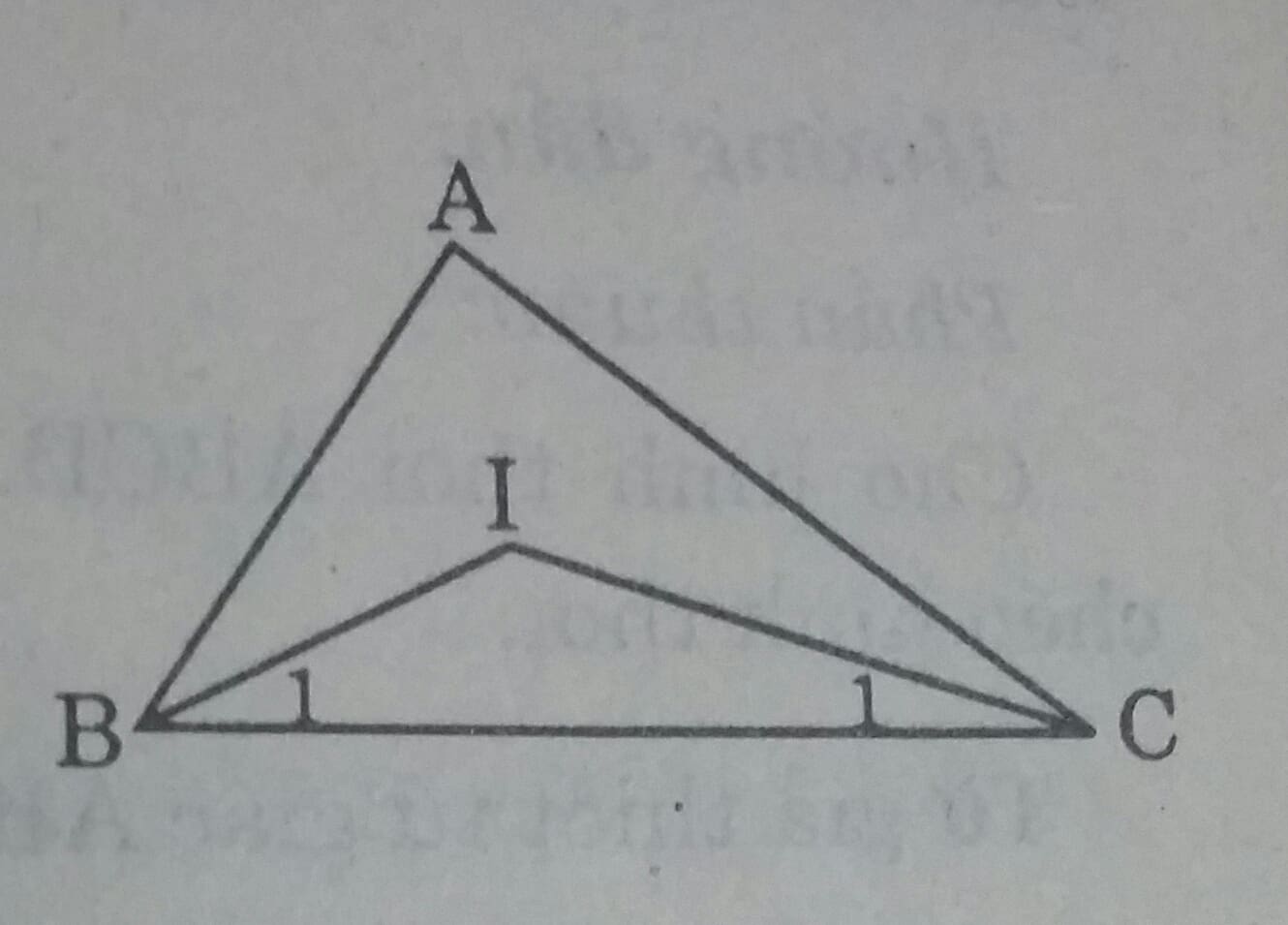
Phần thuận: Xét \(\Delta BIC \ ta \ có:\\ \widehat{BIC}= 180^0 - (\widehat{B}-\widehat{C})= 180^0 - \dfrac{\widehat{B}+\widehat{C}}{2}= 180^0 - \dfrac{90^0}{2}= 135^0 ( \ Vì \Delta ABC \ vuông \ ở \ A)\)
Vậy điểm \(I\) nằm trên hai cung chứa góc \(135^0\) dựng trên đoạn BC ( trừ hai điểm B và C)
Phần đảo:
Lấy điểm \(I\) bất kì trên cung chứa góc \(135^0\) dựng trên đoạn BC ( \(I\) không trùng với B và C)
Vẽ Bx sao cho \(BI\) là tia phân giác của góc \(\widehat{CBx}\).
Vẽ tia Cy sao cho \(CI\) là tia phân giác của góc \(\widehat{BCy}\)
Hai tia Bx và Cy cắt nhau tạo A. Ta phải chứng minh \(\Delta ABC\) vuông tại A. Thật vậy,
Xét
\(\Delta ABC\ ta\ có:\\ \widehat{BAC}= 180^0 - (\widehat{B}+\widehat{C}) = 180^0 - 2( \widehat{B}+\widehat{C}) \)
Xét
\( \Delta BIC \ có\ \widehat{BIC}= 135^0 \)
( vì \(I\) nằm trên cung chứa góc \(135^0\) dựng trên đoạn BC)
Suy ra
\( \widehat{B_1}+\widehat{C_1} = 180^0 - 135^0 = 45^0 \\ Do \ đó \ \widehat{BAC}= 180^0 - 2.45^0 = 90^0 \)
Kết luận: Quỹ tích điểm \(I\) là hai cung chứa góc \(135^0\) dựng trên đoạn thẳng BC ( trừ hai điểm B và C)
Copyright © 2021 HOCTAP247
