Giải bài 47 trang 86 - Sách giáo khoa Toán 9 tập 2

Đề bài

    Gọi cung chứa góc \(55^0\) ở bài tập 46 là cung AmB. Lấy điểm M1 nằm bên trong và điểm M2 nằm bên ngoài đường tròn chứa cung này sao cho M1, M2 và cung AmB nằm cùng một phía đối với đường thẳng AB. Chứng minh rằng:

Hướng dẫn giải

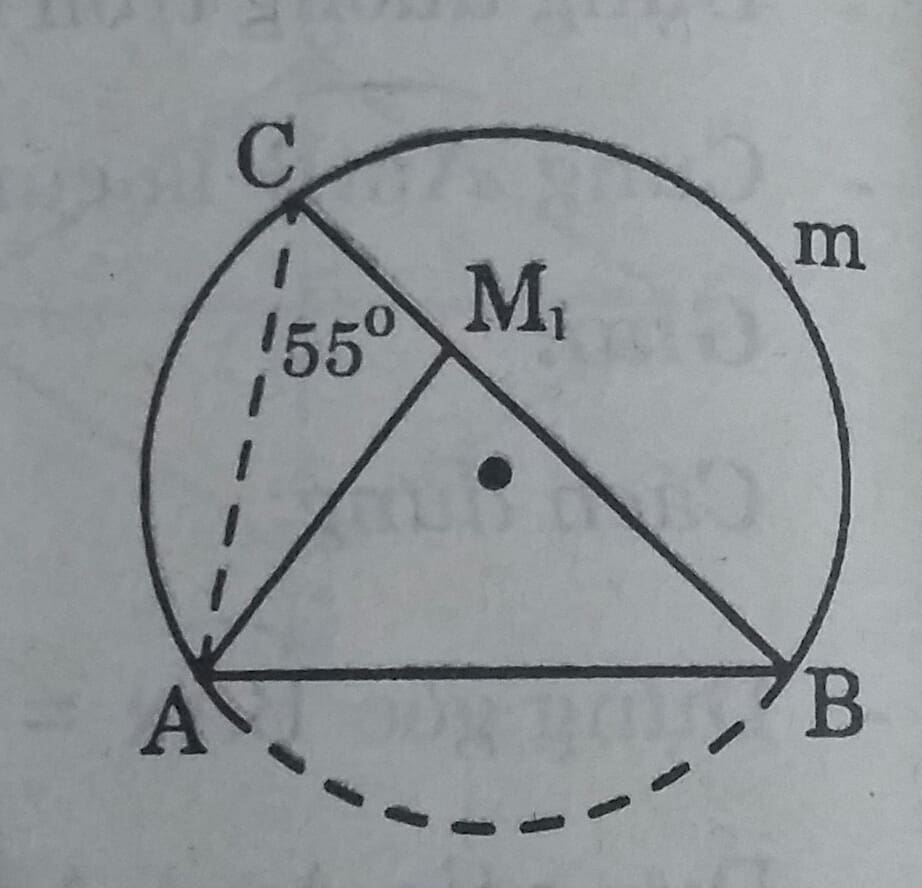
     a) Gọi C là giao điểm của tia \(BM_1 \ và \ cung \stackrel\frown{AmB}\)

   Ta có \( \widehat{ACB}= 55^0\) ( Vì C nằm trên cung chứa góc \(55^0\) dựng trên đoạn AB) 

   Xét \(\Delta M_1AC \ có \ \widehat{AM_1B}\) là góc ngoài tại điểm \(M_1 \ nên \ \widehat{AM_1B}> \widehat{C} \ hay \ \widehat{AM_1B}> 55^0 \)

  b) Gọi C là giao điểm của tia \(BM_1 \ và \ cung \ \stackrel\frown{AmB}\)

 Ta có \( \widehat{ACB}= 55^0\)( Vì C nằm trên cung chứa góc \(55^0\) dựng trên đoạn AB) 

   Xét \(\Delta M_2AC \ có \ \widehat{ABC}\) là góc ngoài tại điểm \(C \ nên \ \widehat{ABC}> \widehat{M_2} \ hay \ \widehat{M_2 }> 55^0 \)

​​​​​​​