Đề kiểm 15 phút - Đề số 7 - Bài 7 - Chương 3 - Hình học 9
Tóm tắt bài
Đề bài
Cho góc \(\widehat {xAy}\) và đường tròn (O tiếp xúc với Ax và Ay tại B và C. Trên đoạn thẳng BC lấy điểm M ( khác B và C). Đường thẳng vuông góc với OM tại M cắt Ax, Ay lần lượt tại D và E. Chứng minh các điểm A, D, O, E cùng nằm trên một đường tròn.
Hướng dẫn giải
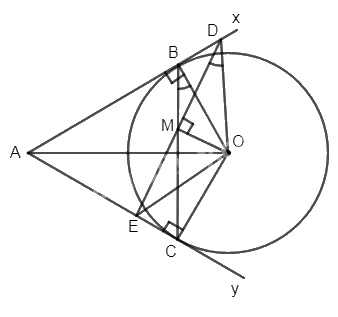
\(Ax \bot OB\) ( tính chất tiếp tuyến) Þ \(\widehat {OBD} = 90^\circ \)
\(\widehat {DMO} = 90^\circ \) (gt) nên tứ giác OMBD nội tiếp.
\( \Rightarrow \widehat {ODM} = \widehat {OBM}\) ( góc nội tiếp cùng chắn cung OM của đường tròn qua O, M, B, D)
Ta lại có tứ giác ABOC nội tiếp nên
\(\widehat {OBM} = \widehat {OAC}\)
\( \Rightarrow \widehat {ODM} = \widehat {OAC}\) hay \(\widehat {ODE} = \widehat {OAE}\).
Vì A, D ở cùng phía đối với EO nên A và D nằm trên một cung chứa góc \(\dfrac{1 }{2}\widehat {xAy}\) dựng trên OE hay A, D, O , E cùng nằm trên một đường tròn.
Copyright © 2021 HOCTAP247
