Luyện tập dấu hiệu nhận biết và chứng minh tứ giác nội tiếp đường tròn
Tóm tắt bài
Luyện tập dấu hiệu nhận biết và chứng minh tứ giác nội tiếp đường tròn
Bài tập về chứng minh tứ giác đã cho nội tiếp là một dạng bài tập rất điển hình, để làm tốt được dạng bài tập này mời các bạn cùng theo dõi bài viết mà chúng tôi đã tổng hợp dưới đây!
I. Tính chất tứ giác nội tiếp
Tứ giác được cho là nội tiếp nếu bốn đỉnh của chúng đều nằm trên một đường tròn. Đường tròn bao quanh tam giác, tứ giác hay các loại đa giác khác ta gọi nó là đường tròn ngoại tiếp, các đỉnh của tứ giác được gọi là đồng viên. Tâm đường tròn được gọi là tâm đường tròn ngoại tiếp và bán kính được gọi là bán kinh đường tròn ngoại tiếp. Các trường hợp thường gặp là tứ giác lồi nội tiếp đường tròn, ngoài ra tứ giác lõm cũng nội tiếp được đường tròn nhưng không phổ biến. Các công thức hoạch ra cũng để áp dụng cho tứ giác lồi là chính.
Trường hợp đặc biệt:
- Các hình đặc biệt như hình vuông, chữ nhật, thoi, thang cân đều nội tiếp.
- Tứ giác lưỡng tâm là tứ giác vừa nội tiếp lại ngoại tiếp đường tròn.
Mới nhất:
II. Dấu hiệu nhận biết tứ giác nội tiếp
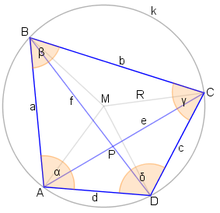
1 - Nếu bốn đường trung trực của bốn cạnh tứ giác đồng quy tại một điểm thì điểm đó chính là tâm đường tròn ngoại tiếp tứ giác.
2 - Dấu hiệu tiếp theo khi hai góc đối bù nhau thì tứ giác ABCD là nội tiếp
\({\displaystyle \alpha +\gamma =\beta +\delta =180^{\circ }.}\) Ở đây \( {\displaystyle \alpha =\widehat{ DAB},\beta =\widehat { ABC},\gamma =\widehat { BCD},\delta =\widehat { CDA}}\)
3 - Từ định lý trên ta đưa ra kết luận như sau: một tứ giác được cho là nội tiếp nếu một góc trong bằng góc ngoài đối diện góc đó.
4 - Nếu tứ giác ABCD có hai góc bằng nhau mà cùng nhìn một cách của tứ giác thì tứ giác ABCD là nội tiếp đường tròn.
Ví dụ như: \({\displaystyle \widehat{ ACB}=\widehat{ ADB}.}\)
5 - Nếu tứ giác đã cho có hai đường chéo bằng tổng của tích hai cặp cạnh đối diện thì tứ giác đã cho là nội tiếp, tức: \({\displaystyle \displaystyle ef=ac+bd.}\)
6 - Nếu hai góc đối diện của tứ giác là góc vuông thì tứ đó là nội tiếp với tâm là trung điềm của hai đường chéo được gắn với hai đỉnh đó.
7 - Nếu hai góc vuông cùa một tứ giác cùng nhìn một cạnh thì tâm đường tròn ngoại tiếp tứ giác đó chính là trung điểm của đường chéo nối liền hai đỉnh đó.
8 - Dấu hiệu khác: \({\displaystyle \tan {\frac {\alpha }{2}}\tan {\frac {\gamma }{2}}=\tan {\frac {\beta }{2}}\tan {\frac {\delta }{2}}=1.}\)
Xem thêm: Tứ giác nội tiếp
III. Bài tập tứ giác nội tiếp
.png)
.png)
Với những lý thuyết bổ ích trên hy vọng các bạn đã hiểu được cách làm dạng bài tập chứng minh này. Nếu còn thắc mắc xin vui lòng để lại dưới mục bình luận. Cảm ơn sự quan tâm của các bạn!
Copyright © 2021 HOCTAP247
