Trang chủ
Lớp 7
Toán Lớp 7 SGK Cũ
Bài 6. Tính chất ba đường phân giác của tam giác
Bài 40 trang 73 SGK Toán 7 tập 2
Bài 40 trang 73 SGK Toán 7 tập 2
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho tam giác ABC cân tại A. gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
Hướng dẫn giải
Áp dụng tính chất ba đường phân giác trong tam giác và trọng tâm của tam giác.
Lời giải chi tiết
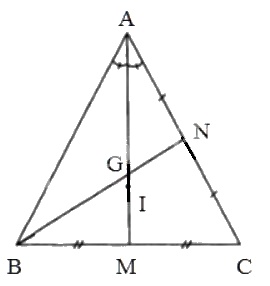
Gọi M, N lần lượt là trung điểm của BC và AC.
Vì G là trọng tâm nên G nằm trên trung tuyến AM (1).
Vì I cách đều ba cạnh của tam giác nên I là giao điểm của ba đường phân giác trong của ΔABC.
ΔABC cân nên đường phân giác xuất phát từ đỉnh đối diện với đáy đồng thời là đường trung tuyến (tính chất trang 71 sgk Toán 7 tập 2). Do đó, I nằm trên AM (2).
Từ (1) và (2) suy ra ba điểm A, G, I thẳng hàng (đpcm).
Copyright © 2021 HOCTAP247
