Giải bài 40 trang 73 - Sách giáo khoa Toán 7 tập 2

Đề bài

Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.

Hướng dẫn giải

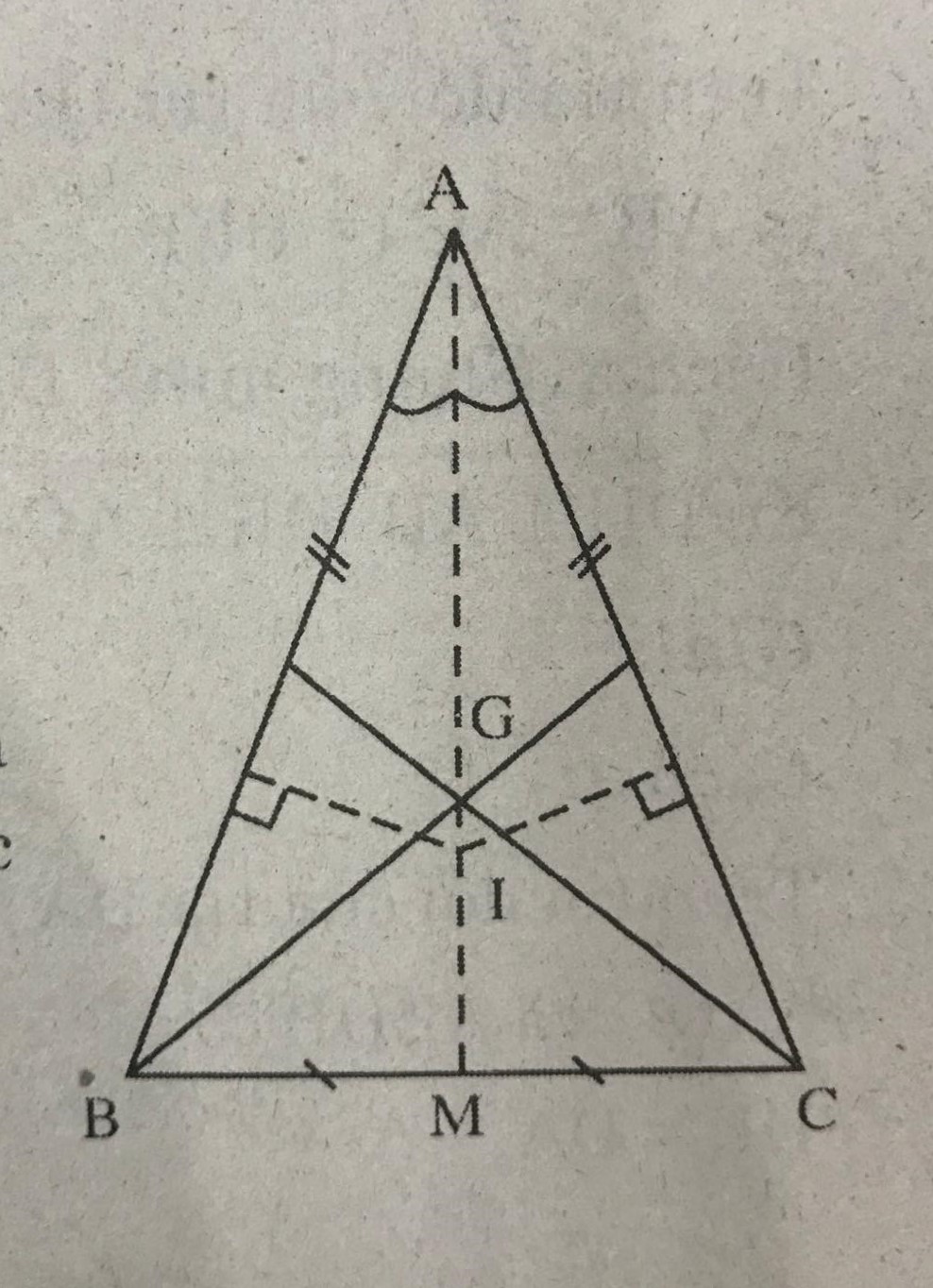
 I nằm trong tam giác và cách đều ba cạnh của tam giác nên AI là tia phân giác của góc \(\widehat{A}\)

 Gọi M là trung điểm của BC.

\(\triangle\)ABC cân tại A nên đường phân giác AI cũng là đường trung tuyến .

Do đó AI đi qua M                       (1)

G là trọng tâm \(\triangle\)ABC nên AM di qua G    (2)

Từ (1) (2) suy ra ba điểm A, I, G thẳng hàng.