Bài 42 trang 73 SGK Toán 7 tập 2

Đề bài

Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.

Gợi ý : Trong ∆ABC, nếu AD vừa là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn AD₁ sao cho DA₁ = AD.

Hướng dẫn giải

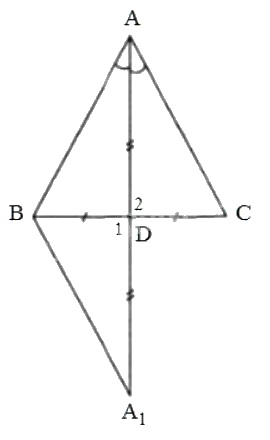
Gọi AD là đường trung tuyến đồng thời là đường phân giác của góc A trong ΔABC.  Ta chứng minh  ∆ABC cân tại A.

Kéo dài AD một đoạn DA₁ = AD

Xét ∆ADC và ∆A₁DB ta có:

DC = DB (do AD là trung tuyến)

\({ \widehat{D}}_1 = {\widehat{D}}_2 \) (2 góc đối đỉnh)

 AD = DA₁ (do cách vẽ)

Vậy ∆ADC =  ∆A₁DB (c.g.c)

\(\Rightarrow \) AC = A₁B        (1)

và \(\widehat{DAC}= \widehat{A_1}\)

Mà \(\widehat{BAD}= \widehat{DAC}\) (gt)

\(\Rightarrow \) \(\widehat{BAD}= \widehat{A_1}\)

Xét tam giác ABA₁ có \(  \widehat{A_1} = \widehat{BAD}\)

Vậy ∆ABA₁ cân tại B 

\(\Rightarrow \) BA = BA₁          (2)

Từ (1) và (2) suy ra AB = AC

Vậy ∆ABC cân tại A.

Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.