Giải bài 42 trang 73 - Sách giáo khoa Toán 7 tập 2

Đề bài

Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.

Hướng dẫn giải

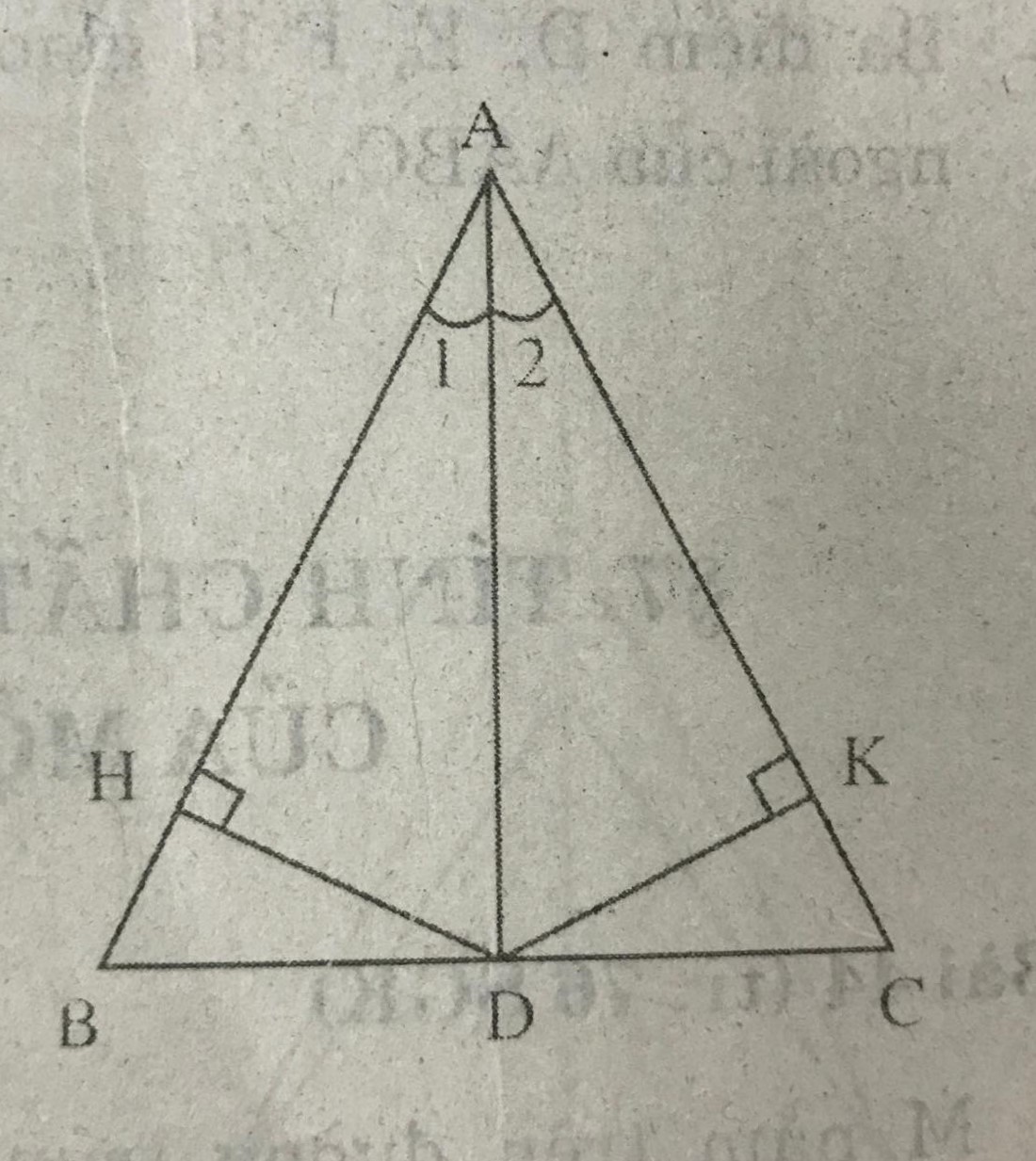
Kẻ DH \(\perp\) AB , DK \(\perp\) AC.

D thuộc tia phân giác của góc A nên DH = DK

\(\triangle\)DHB và \(\triangle\)DKC có :

\(\widehat{H}=\widehat{K}=90^0; DH = DK\)

BD = DC ( AD là trung tuyến của tam giác ABC)

Nên \(\triangle\)DHB = \(\triangle\)DKC (cạnh huyền cạnh góc vuông)

Suy ra : \(\widehat{B}=\widehat{C}\)

Vậy \(\triangle\)ABC là tam giác cân.