Bài 36 trang 123 SGK Toán 9 tập 1

Đề bài

Cho đường tròn tâm \(O\) bán kính \(OA\) và đường tròn đường kính \(OA\).

a) Hãy xác định vị trí tương đối của hai đường tròn.

b) Dây \(AD\) của đường tròn lớn cắt đường tròn nhỏ ở \(C\). Chứng minh rằng \(AC=CD\).

Hướng dẫn giải

a) Cho hai đường tròn \((O;\ R)\) và \((O';\ r)\). Nếu \(OO'=R-r\) thì hai đường tròn tiếp xúc trong.

b) +) Nếu tam giác có cạnh là đường của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.

+) Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó.

Lời giải chi tiết

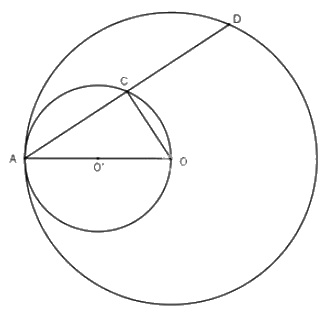
a) Gọi \(O'\) là tâm của đường tròn đường kính \(OA\) thì \(O'A=O'O.\)

Ta có \(OO'=OA-O'A\) hay \(d=R-r\)

Suy ra đường tròn \((O)\) và đường tròn \((O')\) tiếp xúc trong. 

b) Tam giác \(CAO\) có cạnh \(OA\) là đường kính của đường tròn ngoại tiếp nên \(\Delta CAO\) vuông tại \(C\)

\(\Rightarrow OC\perp AD\)

\(\Rightarrow CA=CD\) (đường kính vuông góc với một dây).