Đề kiểm tra 15 phút - Đề số 4 - Bài 8 - Chương 2 - Hình học 9

Đề bài

Cho tam giác ABC vuông tại A có \(AB = 6cm, AC = 8cm\), đường cao AH. Đường tròn (O) đường kính AH cắt AB tại D, đường tròn (O’) đường kính CH cắt AC tại E.

a. Chứng minh (O) và (O’) cắt nhau tại hai điểm phân biệt.

b. Chứng minh đường thẳng DE là tiếp tuyến của (O’).

Hướng dẫn giải

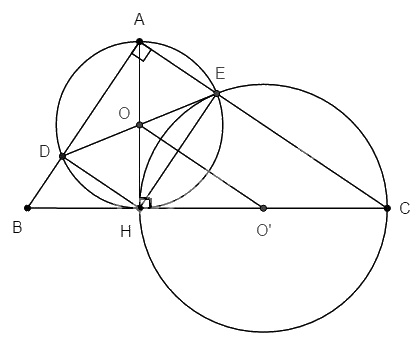
a. ∆ABC vuông tại A, ta có: \(BC = \sqrt {A{B^2} + A{C^2}}  \)\(\;= \sqrt {{6^2} + {8^2}}  = 10\,\left( {cm} \right)\)

Lại có: \(AH.BC = AB.AC\) (hệ thức lượng)

\( \Rightarrow AH = {{AB.AC} \over {BC}} = {{6.8} \over {10}} = 4,8\,\left( {cm} \right)\)

Do đó bán kính của (O) là : \(R = 2,4\) (cm)

Ta có: \(A{C^2} = BC.HC\) (hệ thức lượng)

\( \Rightarrow HC = {{A{C^2}} \over {BC}} = {{{8^2}} \over {10}} = 6,4\,\left( {cm} \right)\)

nên bán kính của (O’) là \(R’ = 3,2cm\)

Mặt khác: OO’ là đường trung bình của ∆AHC

nên \(OO' = {1 \over 2}AC = {1 \over 2}.8 = 4\,\left( {cm} \right)\)

Ta có: \(OO’

b. Ta có: \(\widehat {ADH} = \widehat {AEH} = 90^\circ \) (AH là đường kính) và \(\widehat {BAC} = 90^\circ \) (gt) nên ADHE là hình chữ nhật (có ba góc vuông).

O là giao điểm hai đường chéo AH và \(DE, OH = OE ⇒ ∆OHE\) cân tại O

\( \Rightarrow \widehat {OHE} = \widehat {OEH}\)

Mặt khác, ∆O’HE cân tại O’ (\(O’H = O’E = R’\))

\( \Rightarrow \widehat {O'HE} = \widehat {O'EH},\) mà \(\widehat {OHE} + \widehat {O'HE} = 90^\circ \) (gt)

Do đó \(\widehat {OEH} + \widehat {O'EH} = 90^\circ \) hay \(OE ⊥ O’E\).

\(⇒ DE\) là tiếp tuyến của đường tròn (O’).