Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
Đề kiểm tra 15 phút - Đề số 3 - Bài 8 - Chương 2 - Hình học 9
Đề kiểm tra 15 phút - Đề số 3 - Bài 8 - Chương 2 - Hình học 9
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho đoạn thẳng OO’ và điểm A nằm giữa hai điểm O và O’.
Vẽ đường tròn (O; OA) và đường tròn (O’; O’A). Qua A vẽ đường thẳng cắt (O) tại B và cắt (O’) tại C.
a. Chứng minh (O) và (O’) tiếp xúc nhau.
b. Vẽ đường kính BD của (O) và CE của (O’). Chứng minh D, A, E thẳng hàng.
Hướng dẫn giải
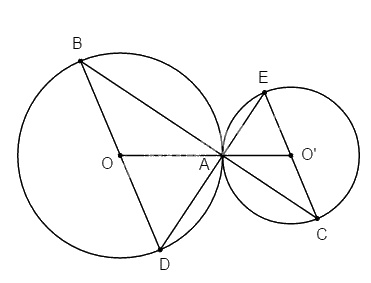
a. Ta có: \(OO’ = OA + O’A \;(d = R + R’)\)
\(⇒\) (O) và (O’) tiếp xúc ngoài tại A.
b. Ta có: BD là đường kính của (O)
nên \(\widehat {BAD} = 90^\circ \Rightarrow DA \bot BA\) hay \(DA \bot BC.\)
Tương tự \(EA ⊥ BC.\)
Vì vậy DA và EA phải trùng nhau hay ba điểm D, A, E thẳng hàng.
Copyright © 2021 HOCTAP247
