Đề kiểm tra 15 phút - Đề số 1 - Bài 8 - Chương 2 - Hình học 9
Tóm tắt bài
Đề bài
Cho nửa đường tròn tâm O, đường kính AB. Trên cùng nửa mặt phẳng bờ là AB, vẽ nửa đường tròn tâm O’ đường kính OA. Vẽ dây cung AC của (O) cắt nửa đường tròn (O’) tại D. Chứng minh:
a. Đường tròn (O) và (O’) tiếp xúc tại A.
b. O’D và OC song song với nhau.
Hướng dẫn giải
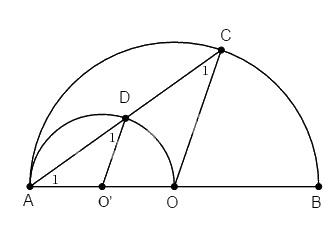
a. Ta có ba điểm A, O’, O thẳng hàng và \(OO’ = OA – O’A \;(d = R – R’)\)
Chứng tỏ (O) và (O’) tiếp xúc trong tại A.
b. Ta có: ∆AO’D cân (vì \(O’A = O’D = R’\)) \( \Rightarrow {\widehat A_1} = {\widehat D_1}\,\left( 1 \right)\)
Tương tự ∆AOC cân \( \Rightarrow {\widehat A_1} = {\widehat C_1}\,\left( 2 \right)\)
Từ (1) và (2) ta có: \({\widehat D_1} = {\widehat C_1}\) ⇒ O’D// OC (cặp góc đồng vị bằng nhau)
Chú ý: Các bạn có thể giải thêm câu c sau đây: Chứng minh D là trung điểm của AC và OD song song với BC.
Hướng dẫn : D thuộc nửa đường tròn đường kính AO nên \(\widehat {ADO} = 90^\circ .\) Khi đó D là trung điểm của AC (định lí đường kính dây cung)
⇒ OD là đường trung bình của ∆AOC, suy ra OD // BC.
Copyright © 2021 HOCTAP247
